题目内容
20.设(3x-1)4=a0+a1x+a2x2+a3x3+a4x4.求:(1)a3
(2)求a0+a1+a2+a3+a4;
(3)求a0+a2+a4;
(4)求各项二项式系数的和.
分析 (1)利用通项公式求出a3
(2)令x=1得,求a0+a1+a2+a3+a4;
(3)令x=-1得,与(2)相加,求a0+a2+a4;
(4)各项二项式系数的和24.
解答 解:(1)a3=${C}_{4}^{1}•{3}^{3}•(-1)$=-108 …(3分)
(2)令x=1得${a_0}+{a_1}+{a_2}+{a_3}+{a_4}={({3-1})^4}=16$;…(6分)
(3)令x=-1得${a_0}-{a_1}+{a_2}-{a_3}+{a_4}={({-3-1})^4}=256$,
而由(2)知:${a_0}+{a_1}+{a_2}+{a_3}+{a_4}={({3-1})^4}=16$,
两式相加得a0+a2+a4=136;…(10分)
(4)各项二项式系数的和为$C_4^0+C_4^1+C_4^2+C_4^3+C_4^4={2^4}=16$.…(14分)
点评 ①要注意二项展开式各项的系数与二项式系数是不同的两个概念;②系数和与二项式系数和不一定相同,本题的(1)与(5)结果相同纯属巧合;③注意求系数和上述是最一般的方法,一定要理解.

练习册系列答案
相关题目
6.已知i是虚数单位,则2i(1+i)=( )
| A. | -2+2i | B. | 2+2i | C. | 2i | D. | -2i |
8.在△ABC中,边 a,b,c的对应角分别为A,B,C.若a=1,b=$\sqrt{3},A={30°}$,则B等于( )
| A. | 60° | B. | 60°或120° | C. | 30°或150° | D. | 120° |
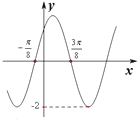 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0≤φ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)=2sin(2x+$\frac{π}{4}$).