题目内容
抛物线y2=2px(p>0)上点M到定点A(3,2)和焦点F的距离之和的最小值为5,求此抛物线的方程.
抛物线方程为y2=8x.
若A(3,2)在抛物线内,设l为准线,作AN⊥l于点N,交抛物线于点M,
则|MN|+|MA|=|MA|+|MF|=5.
∴(xm+
)+(3-xm)=5.
∴p=4.
若A(3,2)在抛物线外,连线AF交抛物线于点M,则|AM|+|MF|=|AF|=
=5.
∴p=6±2
.
又A(3,2)在抛物线外,
∴4>y2=6p.
∴0<p<
.
∴p=6±2不合题意.
综上,p=4,所求抛物线方程为y2=8x.
则|MN|+|MA|=|MA|+|MF|=5.
∴(xm+
)+(3-xm)=5.∴p=4.
若A(3,2)在抛物线外,连线AF交抛物线于点M,则|AM|+|MF|=|AF|=
=5.∴p=6±2
.又A(3,2)在抛物线外,
∴4>y2=6p.
∴0<p<
.∴p=6±2
不合题意.综上,p=4,所求抛物线方程为y2=8x.
练习册系列答案
相关题目
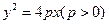的准线与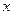
轴交点为
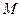，过点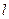
交抛物线与不同的点
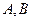两点.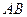
中点的轨迹方程；
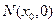，求证：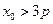
.
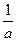x2(a≠0)的焦点坐标是__________.
·
等于( )
B.-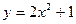
上运动，则P点与点A(0,-1)所连线段中点M的轨迹方程是