题目内容
2. 在某中学举行的环保知识竞赛中,随机抽取x名参赛同学的成绩(得分的整数)进行整理后分成五组,绘制出如图所示的频率分布直方图,已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05,第二小组的频数为40.
在某中学举行的环保知识竞赛中,随机抽取x名参赛同学的成绩(得分的整数)进行整理后分成五组,绘制出如图所示的频率分布直方图,已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05,第二小组的频数为40.(1)求第二小组的频率,并补全这个频率分布直方图,画出频率分布折线图;
(2)若采用分层抽样的方法,从样本中随机取20人,则第三组和第四组各抽取多少人?
(3)在(2)的条件下,从第三组和第四组抽取的人中任选取2人,则她们不在同一组别的概率是多少?
分析 (1)由各小组的频率之和为1,第一、三、四、五组的频率分别是0.3,0.15,0.10,0.05,能求出第二小组的频率和第二小组的小长方形的高,由此可补全频率分布直方图(图阴影部分)和频率分布折线图.
(2)由第二小组的频数为40,频率为0.40,由频率=$\frac{频数}{总数}$,能求出第三组抽取的人数和第四组抽取的人数.
(3)用a1,a2,a3表示第三组抽取的三位学生,第四组抽取的二位学生用b1,b2表示,利用列举法求出所有的基本事件和满足条件的基本事件,由此能求出第三组和第四组抽取的人中任选取2人,她们不在同一组别的概率.
解答 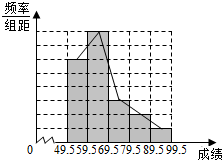 (本小题满分12分)
(本小题满分12分)
解:(1)因为各小组的频率之和为1,第一、三、四、五组的频率分别是0.3,0.15,0.10,0.05,
所以第二小组的频率为1-(0.30+0.15+0.10+0.05)=0.40.…(2分)
因为第二小组的频率为0.40,
所以落在59.5-69.5的第二小组的小长方形的高=$\frac{频率}{组距}$=$\frac{0.4}{10}$=0.04,
由此可补全频率分布直方图(图阴影部分)和频率分布折线图如右图所示.…(4分)
(2)因为第二小组的频数为40,频率为0.40,
所以$\frac{40}{x}=0.40$,得x=100(人).…(6分)
所以第三组抽取的人数为$\frac{20}{100}×100×0.15=3$(人),
第四组抽取的人数为$\frac{20}{100}×100×0.10=2$(人).…(8分)
(3)用a1,a2,a3表示第三组抽取的三位学生,第四组抽取的二位学生用b1,b2表示,
则所有的基本事件为:(a1,a2)、(a1,a3),(a1,b1)、(a1,b2)、(a2,a3)、(a2,b1)、(a2,b2)、(a3,b1)、(a3,b2)、(b1,b2),共10种.…(10分)
其中满足条件的基本事件为:(a1,b1)、(a1,b2)、(a2,b1)、(a2,b2)、(a3,b1)、(a3,b2),共6种.…(11分)
所以所求概率为p=$\frac{6}{10}$=$\frac{3}{5}$.…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1 | B. | 0.875 | C. | 0.65 | D. | 0.5 |

| A. | $\frac{7}{3}π$ | B. | $\frac{10}{3}π$ | C. | 4π | D. | 5π |
 执行如图的程序框图,若p=7,则输出的s=$\frac{3}{8}$.
执行如图的程序框图,若p=7,则输出的s=$\frac{3}{8}$.