题目内容
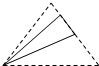
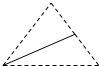
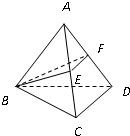
 如图,设四面体ABCD各棱长均相等,E、F分别为AC,AD中点,则△BEF在该四面体的面ABC上的射影是下图中的
如图,设四面体ABCD各棱长均相等,E、F分别为AC,AD中点,则△BEF在该四面体的面ABC上的射影是下图中的
- A.

- B.

- C.

- D.

B
分析:由于是正四面体,不难得到D在ABC上的射影,即可得到AD在ABC上的射影,即可推出正确选项.
解答: 解:由于几何体是正四面体,
解:由于几何体是正四面体,
所以D在ABC上的射影是它的中心,可得到AD在ABC上的射影,
因为F在AD上,所以考察选项,只有B正确.
故选B.
点评:本题是基础题,考查射影问题,明确几何体的结构特征,是解好这类问题的关键,考查空间想象能力,逻辑思维能力.
分析:由于是正四面体,不难得到D在ABC上的射影,即可得到AD在ABC上的射影,即可推出正确选项.
解答:
 解:由于几何体是正四面体,
解:由于几何体是正四面体,所以D在ABC上的射影是它的中心,可得到AD在ABC上的射影,
因为F在AD上,所以考察选项,只有B正确.
故选B.
点评:本题是基础题,考查射影问题,明确几何体的结构特征,是解好这类问题的关键,考查空间想象能力,逻辑思维能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 10、如图,设四面体ABCD各棱长均相等,E、F分别为AC,AD中点,则△BEF在该四面体的面ABC上的射影是下图中的( )
10、如图,设四面体ABCD各棱长均相等,E、F分别为AC,AD中点,则△BEF在该四面体的面ABC上的射影是下图中的( )