题目内容
 设全集U是实数集R,M={x||x|>2},N={x|4x-3-x2>0},则图中阴影部分所表示的集合是( )
设全集U是实数集R,M={x||x|>2},N={x|4x-3-x2>0},则图中阴影部分所表示的集合是( )分析:先求出集合M,N,然后求出图中阴影部分所表示的集合为(CUM)∩N可求
解答:解:由题意可得,M={x||x|>2}={x|x>2或x<-2},N={x|4x-3-x2>0}={x|1<x<3}
∵图中阴影部分所表示的集合为(CUM)∩N={x}-2≤x≤2}∩{x|1<x<3}={x|1<x≤2}
故选C
∵图中阴影部分所表示的集合为(CUM)∩N={x}-2≤x≤2}∩{x|1<x<3}={x|1<x≤2}
故选C
点评:本题主要考查了利用维恩图表示集合的基本关系,及绝对值不等式、二次不等式的求解,属于基础试题

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 设全集U是实数集R,M={x|x2>4},N={x|
设全集U是实数集R,M={x|x2>4},N={x|| 2 |
| x-1 |
| A、{x|-2≤x<1} |
| B、{x|-2≤x≤2} |
| C、{x|1<x≤2} |
| D、{x|x<2} |
 设全集U是实数集R,M={x||x|≥2},N={x|1<x<3},则图中阴影部分所表示的集合是( )
设全集U是实数集R,M={x||x|≥2},N={x|1<x<3},则图中阴影部分所表示的集合是( )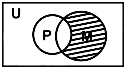 设全集U是实数集R,M={x|x<-1,或x>2},P={x|x<1或x>5},则图中阴部分所表示的集合是( )
设全集U是实数集R,M={x|x<-1,或x>2},P={x|x<1或x>5},则图中阴部分所表示的集合是( ) 设全集U是实数集R,
设全集U是实数集R, (2010•台州一模)设全集U是实数集R,M={x|x2>4},N={x|y=lg(x2-4x+3)},则图中阴影部分所表示的集合是
(2010•台州一模)设全集U是实数集R,M={x|x2>4},N={x|y=lg(x2-4x+3)},则图中阴影部分所表示的集合是