题目内容
P为椭圆 上一点,F1、F2是椭圆的左、右焦点,若使△F1PF2为直角三角形的点P共有8个,则椭圆离心率的取值范围是( )
上一点,F1、F2是椭圆的左、右焦点,若使△F1PF2为直角三角形的点P共有8个,则椭圆离心率的取值范围是( )A.

B.

C.

D.

【答案】分析:由题意有可得,以F1F2为直径的圆与椭圆有4个交点,求得当点P在y轴上时,e= ,从而得到满足条件的
,从而得到满足条件的  <e<1.
<e<1.
解答:解:由题意有可得,以F1F2为直径的圆与椭圆有4个交点,
又离心率越大,椭圆越扁,当点P在y轴上时,b=c,
椭圆离心率为e= =
= =
= ,
,
∴满足条件的 <e<1,
<e<1,
故选 A.
点评:本题考查椭圆的标准方程,以及简单性质的应用,求出当点P在y轴上时,e= ,是解题的关键.
,是解题的关键.
 ,从而得到满足条件的
,从而得到满足条件的  <e<1.
<e<1.解答:解:由题意有可得,以F1F2为直径的圆与椭圆有4个交点,
又离心率越大,椭圆越扁,当点P在y轴上时,b=c,
椭圆离心率为e=
 =
= =
= ,
,∴满足条件的
 <e<1,
<e<1,故选 A.
点评:本题考查椭圆的标准方程,以及简单性质的应用,求出当点P在y轴上时,e=
 ,是解题的关键.
,是解题的关键. 
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目





 上一点,F1,F2是椭圆的焦点,∠F1PF2=900,则△F1PF2的面积为___________;
上一点,F1,F2是椭圆的焦点,∠F1PF2=900,则△F1PF2的面积为___________;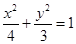 上一点,F1、F2为该椭圆的两个焦点,若
上一点,F1、F2为该椭圆的两个焦点,若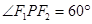 ,则
,则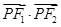 =(
)
=(
)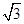 C.
C. D.2
D.2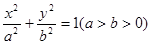 上一点,F1、F2是椭圆的左、右焦点,若使△F1PF2为直角三角形的点P共有8个,则椭圆离心率的取值范围是 ▲
上一点,F1、F2是椭圆的左、右焦点,若使△F1PF2为直角三角形的点P共有8个,则椭圆离心率的取值范围是 ▲
 上一点,F1、F2为左右焦点,∠F1PF2=90°
上一点,F1、F2为左右焦点,∠F1PF2=90° ;
;