题目内容
中心在原点,焦点在x轴上的双曲线C1的离心率为e,直线l与双曲线C1交于A,B两点,线段AB中点M在一象限且在抛物线y2=2px(p>0)上,且M到抛物线焦点的距离为p,则l的斜率为( )
分析:利用抛物线的定义,确定M的坐标,利用点差法将线段AB中点M的坐标代入,即可求得结论.
解答:解:∵M在抛物线y2=2px(p>0)上,且M到抛物线焦点的距离为p,
∴M的横坐标为
,∴M(
,p)
设双曲线方程为
-
=1(a>0,b>0),A(x1,y1),B(x2,y2),则
-
=1,
-
=1
两式相减,并将线段AB中点M的坐标代入,可得
-
=0
∴
=
∴
=
=
故选A.
∴M的横坐标为
| p |
| 2 |
| p |
| 2 |
设双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
| x12 |
| a2 |
| y12 |
| b2 |
| x22 |
| a2 |
| y22 |
| b2 |
两式相减,并将线段AB中点M的坐标代入,可得
| p(x1-x2) |
| a2 |
| 2p(y1-y2) |
| b2 |
∴
| y1-y2 |
| x1-x2 |
| b2 |
| 2a2 |
∴
| y1-y2 |
| x1-x2 |
| a2-c2 |
| 2a2 |
| e2-1 |
| 2 |
故选A.
点评:本题考查双曲线与抛物线的综合,考查点差法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
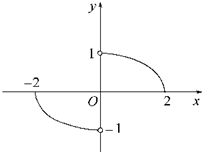 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|
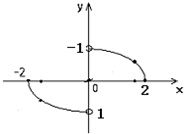 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
 .
.