题目内容
定义在R上的函数f(x)满足:①是偶函数;②对任意的x1、x2都有 .请写出这样的一个函数f(x)= .
.请写出这样的一个函数f(x)= .
【答案】分析:先利用奇偶性,再有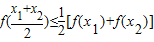 可判断函数可为凸函数,故只要写一个即可.
可判断函数可为凸函数,故只要写一个即可.
解答:解:由于定义在R上的函数f(x)对任意的x1、x2都有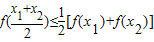 ,故函数为凸函数,
,故函数为凸函数,
又由函数为偶函数,故满足条件的一个函数为f(x)=x2+b
故答案为 x2+b
点评:本题考查了抽象函数表达式反映函数性质的意义和应用,属于基础题.
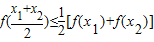 可判断函数可为凸函数,故只要写一个即可.
可判断函数可为凸函数,故只要写一个即可.解答:解:由于定义在R上的函数f(x)对任意的x1、x2都有
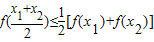 ,故函数为凸函数,
,故函数为凸函数,又由函数为偶函数,故满足条件的一个函数为f(x)=x2+b
故答案为 x2+b
点评:本题考查了抽象函数表达式反映函数性质的意义和应用,属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目