题目内容
已知函数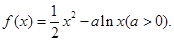
(Ⅰ)若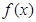 在
在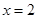 处的切线与直线
处的切线与直线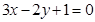 平行,求
平行,求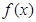 的单调区间;
的单调区间;
(Ⅱ)求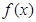 在区间
在区间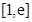 上的最小值.
上的最小值.
【答案】
(Ⅰ)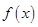 的单调递减区间是(
的单调递减区间是(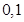 ),单调递增区间是
),单调递增区间是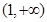 ;(Ⅱ)当
;(Ⅱ)当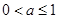 时,
时,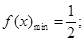 当
当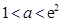 时,
时,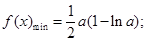 当
当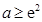 时,
时,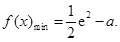 .
.
【解析】
试题分析:(Ⅰ)若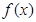 在
在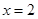 处的切线与直线
处的切线与直线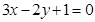 平行,与函数曲线的切线有关,可利用导数的几何意义来解,既对
平行,与函数曲线的切线有关,可利用导数的几何意义来解,既对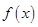 求导即可,本题由函数
求导即可,本题由函数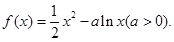 ,知
,知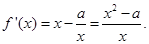 ,由
,由
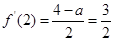 ,能求出
,能求出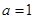 ,要求
,要求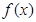 的单调区间,先求出函数的定义域,求出导函数,令导函数大于
的单调区间,先求出函数的定义域,求出导函数,令导函数大于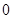 ,求出
,求出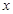 的范围,写出区间形式即得到函数
的范围,写出区间形式即得到函数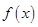 的单调增区间;(II)求
的单调增区间;(II)求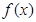 在区间
在区间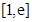 上的最小值,求出导函数,令导函数为
上的最小值,求出导函数,令导函数为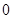 求出根,通过讨论根与区间
求出根,通过讨论根与区间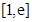 的关系,判断出函数的单调性,求出函数的最小值.
的关系,判断出函数的单调性,求出函数的最小值.
试题解析:(Ⅰ)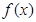 的定义域为
的定义域为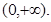
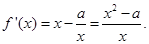
由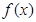 在
在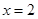 处的切线与直线
处的切线与直线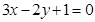 平行,
平行,
则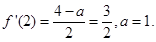 4分
4分
此时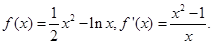 令
令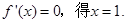
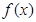 与
与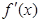 的情况如下:
的情况如下:
|
|
( |
1 |
|
|
|
— |
0 |
+ |
|
|
↘ |
|
↗ |
所以,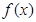 的单调递减区间是(
的单调递减区间是(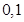 ),单调递增区间是
),单调递增区间是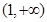 7分
7分
(Ⅱ)由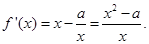
由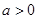 及定义域为
及定义域为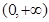 ,令
,令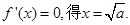
①若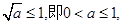 在
在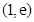 上,
上,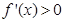 ,
,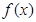 在
在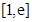 上单调递增,
上单调递增,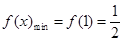 ;
;
②若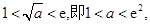 在
在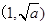 上,
上,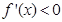 ,
,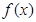 单调递减;在
单调递减;在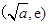 上,
上,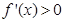 ,
,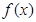 单调递增,因此在
单调递增,因此在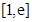 上,
上,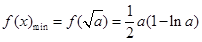 ;
;
③若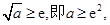 在
在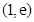 上,
上,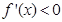 ,
,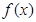 在
在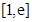 上单调递减,
上单调递减, 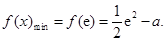
综上,当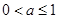 时,
时,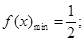 当
当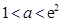 时,
时,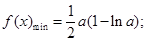
当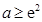 时,
时,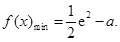 14分
14分
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
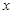
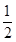
 .
. 在区间
在区间 单调递增,求
单调递增,求 的最小值;
的最小值; ,对
,对 ,使
,使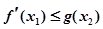 成立,求
成立,求 的范围.
的范围.
 在区间[1,+∞)上是增函数,求实数a的取值范围;
在区间[1,+∞)上是增函数,求实数a的取值范围; 是
是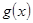 =bx的图象与函数
=bx的图象与函数