题目内容
已知函数f(x)=alnx-ax-3(a∈R).
(1)若a=-1,求函数f(x)的单调区间并比较f(x)与f(1)的大小关系
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数 在区间(t,3)上总不是单调函数,求m的取值范围.
在区间(t,3)上总不是单调函数,求m的取值范围.
解:(1)当a=-1时, ,
,
解f'(x)>0,得x∈(1,+∞);解f'(x)<0得x∈(0,1),
所以,f(x)的单调增区间为(1,+∞),减区间为(0,1),
可知f(x)min=f(1),所以f(x)≥f(1).
(2)∵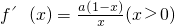 ,函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,
,函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,
∴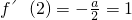 ,得a=-2,f(x)=-2lnx+2x-3,
,得a=-2,f(x)=-2lnx+2x-3,
∴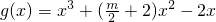 ,∴g'(x)=3x2+(m+4)x-2,
,∴g'(x)=3x2+(m+4)x-2,
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2,∴ ,
,
由题意知:对于任意的t∈[1,2],g'(t)<0恒成立,
所以有,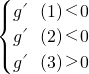 ,解得
,解得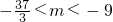 .
.
故m的取值范围为( ,-9).
,-9).
分析:(1)当a=-1时,求出f′(x),解不等式f′(x)>0,f′(x)<0,可得单调区间,根据最值情况可比较f(x)与f(1)的大小关系;
(2)由函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,可求出a值,对于任意的t∈[1,2],函数g(x)在区间(t,3)上总不单调,则g(x)在区间(t,3)内总存在极值点,由此可得到关于m的约束条件,解出即可.
点评:本题考查导数的几何意义、利用导数研究函数的单调性以及恒成立问题,考查分析问题解决问题的能力.
 ,
,解f'(x)>0,得x∈(1,+∞);解f'(x)<0得x∈(0,1),
所以,f(x)的单调增区间为(1,+∞),减区间为(0,1),
可知f(x)min=f(1),所以f(x)≥f(1).
(2)∵
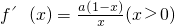 ,函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,
,函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,∴
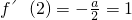 ,得a=-2,f(x)=-2lnx+2x-3,
,得a=-2,f(x)=-2lnx+2x-3,∴
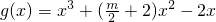 ,∴g'(x)=3x2+(m+4)x-2,
,∴g'(x)=3x2+(m+4)x-2,∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2,∴
 ,
,由题意知:对于任意的t∈[1,2],g'(t)<0恒成立,
所以有,
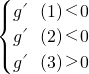 ,解得
,解得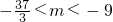 .
.故m的取值范围为(
 ,-9).
,-9).分析:(1)当a=-1时,求出f′(x),解不等式f′(x)>0,f′(x)<0,可得单调区间,根据最值情况可比较f(x)与f(1)的大小关系;
(2)由函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,可求出a值,对于任意的t∈[1,2],函数g(x)在区间(t,3)上总不单调,则g(x)在区间(t,3)内总存在极值点,由此可得到关于m的约束条件,解出即可.
点评:本题考查导数的几何意义、利用导数研究函数的单调性以及恒成立问题,考查分析问题解决问题的能力.

练习册系列答案
相关题目