题目内容
(本小题满分12分)
如果两个椭圆的离心率相等,那么就称这两个椭圆相似.已知椭圆 与椭圆
与椭圆 相似,且椭圆
相似,且椭圆 的一个短轴端点是抛物线
的一个短轴端点是抛物线 的焦点.
的焦点.
(Ⅰ)试求椭圆 的标准方程;
的标准方程;
(Ⅱ)设椭圆 的中心在原点,对称轴在坐标轴上,直线
的中心在原点,对称轴在坐标轴上,直线 与椭圆
与椭圆 交于
交于 两点,且与椭圆
两点,且与椭圆 交于
交于 两点.若线段
两点.若线段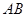 与线段
与线段 的中点重合,试判断椭圆
的中点重合,试判断椭圆 与椭圆
与椭圆 是否为相似椭圆?并证明你的判断.
是否为相似椭圆?并证明你的判断.
(Ⅰ)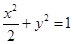 .(Ⅱ)椭圆
.(Ⅱ)椭圆 与椭圆
与椭圆 是相似椭圆. 证明见解析。
是相似椭圆. 证明见解析。
解析试题分析:(Ⅰ)椭圆 的离心率为
的离心率为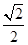 , 抛物线
, 抛物线 的焦点为
的焦点为 .
.
设椭圆 的方程为
的方程为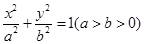 ,由题意,得:
,由题意,得: 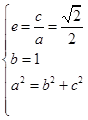 ,解得
,解得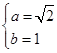 ,
,
∴椭圆 的标准方程为
的标准方程为 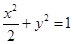 . ………………………………4分
. ………………………………4分
(Ⅱ)解法一:椭圆 与椭圆
与椭圆 是相似椭圆. ………………………………5分
是相似椭圆. ………………………………5分
联立 和
和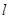 的方程,
的方程,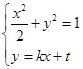 ,消去
,消去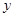 ,得
,得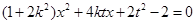 , ……6分
, ……6分
设 的横坐标分别为
的横坐标分别为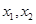 ,则
,则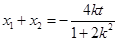 .
.
设椭圆 的方程为
的方程为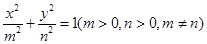 , …………………………………7分
, …………………………………7分
联立方程组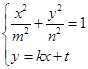 ,消去
,消去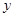 ,得
,得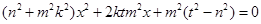 ,
,
设 的横坐标分别为
的横坐标分别为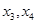 ,则
,则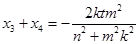 .
.
∵弦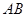 的中点与弦
的中点与弦 的中点重合,∴
的中点重合,∴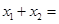
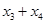 ,
,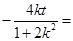
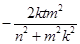 ,
,
∵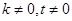 ,∴化简得
,∴化简得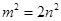 , ……………………………10分
, ……………………………10分
求得椭圆 的离心率
的离心率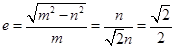 , ………………………12分
, ………………………12分
∴椭圆 与椭圆
与椭圆 是相似椭圆.
是相似椭圆.
解法二:(参照解法1评分)
设椭圆 的方程为
的方程为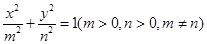 ,
,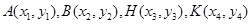 .
.
∵ 在椭圆
在椭圆 上,∴
上,∴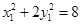 且
且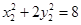 ,两式相减并恒等变形得
,两式相减并恒等变形得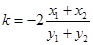 .
.
由 在椭圆
在椭圆 上,仿前述方法可得
上,仿前述方法可得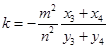 .
.
∵弦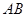 的中点与弦
的中点与弦 的中点重合,
的中点重合,
∴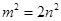 ,求得椭圆
,求得椭圆 的离心率
的离心率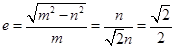 , 即椭圆
, 即椭圆 与椭圆
与椭圆 是相似椭圆.
是相似椭圆.
考点:本题主要考查椭圆的标准方程,椭圆的几何性质,直线与椭圆的位置关系。
点评:综合题,判断椭圆 与椭圆
与椭圆 是否为相似椭圆,主要是要把握好“如果两个椭圆的离心率相等,那么就称这两个椭圆相似”这一定义,“点差法”是常用方法.
是否为相似椭圆,主要是要把握好“如果两个椭圆的离心率相等,那么就称这两个椭圆相似”这一定义,“点差法”是常用方法.

练习册系列答案
相关题目
 的中心为直角坐标系
的中心为直角坐标系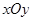 的原点,焦点在
的原点,焦点在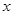 轴上,它的一个顶点到两个焦点的距离分别是7和1
轴上,它的一个顶点到两个焦点的距离分别是7和1 为椭圆
为椭圆 为过
为过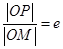 (e为椭圆C的离心率),求点
(e为椭圆C的离心率),求点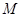 经过定点
经过定点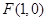 ,且与直线
,且与直线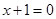 相切。
相切。 方程;
方程;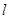 过定点
过定点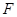 与曲线
与曲线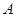 、
、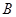 两点:
两点: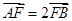 ,求直线
,求直线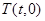 始终在以
始终在以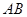 为直径的圆内,求
为直径的圆内,求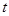 的取值范围。
的取值范围。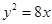 的焦点,M的离心率
的焦点,M的离心率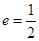 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线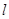 ,交M于A,B两点。
,交M于A,B两点。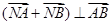 ,求实数t的取值范围。
,求实数t的取值范围。 ,并经过点
,并经过点 ,求此双曲线的标准方程.
,求此双曲线的标准方程.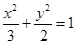 的左、右顶点分别为
的左、右顶点分别为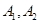 ,点M是椭圆上异于
,点M是椭圆上异于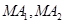 的斜率分别为
的斜率分别为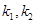 ,求证
,求证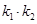 为定值并求出此定值;
为定值并求出此定值;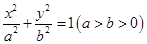 的左、右顶点分别为
的左、右顶点分别为 的双曲线的方程.
的双曲线的方程.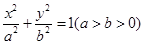 的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。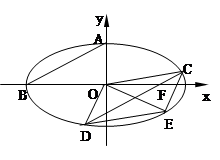
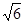 , 求椭圆的方程.
, 求椭圆的方程.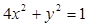 及直线
及直线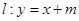 ,当直线和椭圆有公共点时.
,当直线和椭圆有公共点时.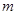 的取值范围;
的取值范围;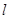 的方程.
的方程.