题目内容
 已知AB=2,AD=2
已知AB=2,AD=2| 2 |
求:
(1)三角形PCD的面积;
(2)异面直线BC与AE所成的角的大小.
分析:(1)因为PA⊥底面ABCD,所以PA⊥CD,又AD⊥CD,所以CD⊥平面PAD,由此能求出三角形PCD的面积.
(2)取PB中点F,连接EF、AF,则EF∥BC,从而∠AEF(或其补角)是异面直线BC与AE所成的角,由此能求出异面直线BC与AE所成的角的大小.
(2)取PB中点F,连接EF、AF,则EF∥BC,从而∠AEF(或其补角)是异面直线BC与AE所成的角,由此能求出异面直线BC与AE所成的角的大小.
解答:解: (1)∵PA⊥底面ABCD,
(1)∵PA⊥底面ABCD,
∴PA⊥CD,
又∵AD⊥CD,∴CD⊥平面PAD,
从而CD⊥PD,
∵PD=
=2
,CD=2,
∴三角形PCD的面积为
×2×2
=2
.…(6分)
(2)取PB中点F,连接EF、AF,则EF∥BC,
∴∠AEF(或其补角)是异面直线BC与AE所成的角,
在△AEF中,∵EF=
,AF=
,AE=2,
∴△AEF是等腰直角三角形,
所以∠AEF=
.…(6分)
 (1)∵PA⊥底面ABCD,
(1)∵PA⊥底面ABCD,∴PA⊥CD,
又∵AD⊥CD,∴CD⊥平面PAD,
从而CD⊥PD,
∵PD=
22+(2
|
| 3 |
∴三角形PCD的面积为
| 1 |
| 2 |
| 3 |
| 3 |
(2)取PB中点F,连接EF、AF,则EF∥BC,
∴∠AEF(或其补角)是异面直线BC与AE所成的角,
在△AEF中,∵EF=
| 2 |
| 2 |
∴△AEF是等腰直角三角形,
所以∠AEF=
| π |
| 4 |
点评:本题考查三角形面积的求法,考查异面直线所成角的求法,解题时要认真审题,注意合理地化空问题为平面问题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
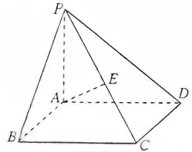 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知AB=2,AD=2 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,