题目内容
13.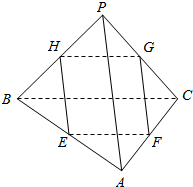 如图所示,在三棱锥P-ABC中,PA=4,BC=6,与PA、BC都平行的截面四边形EFGH的周长为l,试确定l的取值范围.
如图所示,在三棱锥P-ABC中,PA=4,BC=6,与PA、BC都平行的截面四边形EFGH的周长为l,试确定l的取值范围.
分析 由已知得PA∥EH,PA∥FG,BC∥EF,BC∥HG,从而四边形EFGH的周长l=2(EF+FG)=8+$\frac{4AE}{AB}$,由0<$\frac{AE}{AB}$<1,能求出l的取值范围.
解答  解:∵PA∥平面EFGH,PA?平面PAB,
解:∵PA∥平面EFGH,PA?平面PAB,
平面PAB∩平面EFGH=EH,
∴PA∥EH,
同理,PA∥FG,BC∥EF,BC∥HG,
∴$\frac{EF}{BC}=\frac{AE}{AB}$,EF=$\frac{AE•BC}{AB}$,$\frac{FG}{AP}=\frac{CF}{CA}=\frac{BE}{BA}$,
FG=$\frac{BE•AP}{BA}$,
∴四边形EFGH的周长:
l=2(EF+FG)
=$\frac{2(AE•BC+BE•AP)}{AB}$
=$\frac{12AE+8BE}{AB}$
=$\frac{8AB+4AE}{AB}$
=8+$\frac{4AE}{AB}$,
∵0<$\frac{AE}{AB}$<1,
∴8<l<12.
∴l的取值范围是(8,12).
点评 本题考查截面四边形的周长的取值范围的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
4.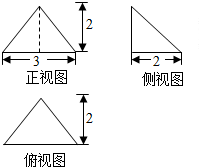 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )
 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )| A. | 6 | B. | 18 | C. | 8+3$\sqrt{2}$ | D. | 3+4$\sqrt{13}$ |
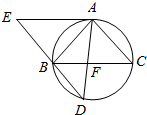 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$. 已知某公司准备投资一个项目,为慎重起见,该公司提前制定了两套方案,并召集了各部门的经理对这两套方案进行研讨,并对认为合理的方案进行了投票表决,统计结果如茎叶图所示,试说明方案比较稳妥的是第一套方案.
已知某公司准备投资一个项目,为慎重起见,该公司提前制定了两套方案,并召集了各部门的经理对这两套方案进行研讨,并对认为合理的方案进行了投票表决,统计结果如茎叶图所示,试说明方案比较稳妥的是第一套方案.