题目内容
三次函数f(x)=x3-3bx+3b在[1,2]内恒为正值,求b的取值范围.
分析:由f(x)>0在[1,2]内恒成立,即3b(x-1)<x3.对x分类讨论:①当x=1时,上式对于b∈R都成立;②当1<x≤2时,f(x)>0在[1,2]内恒成立?3b<
恒成立?3b<[
]min,x∈(1,2],利用导数求出其最小值即可.
| x3 |
| x-1 |
| x3 |
| x-1 |
解答:解:由f(x)>0在[1,2]内恒成立,即3b(x-1)<x3.
①当x=1时,上式对于b∈R都成立;
②当1<x≤2时,f(x)>0在[1,2]内恒成立?3b<
恒成立,x∈(1,2]?3b<[
]min,x∈(1,2].
令g(x)=
,x∈(1,2],则g′(x)=
,由g′(x)=0,解得x=
.
列表如下: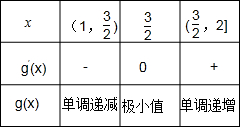
由表格可知:当x=
时,g(x)取得极小值,也即最小值,g(
)=
=
.
∴3b<
,解得b<
.
综上①②可知:b的取值范围是(-∞,
).
①当x=1时,上式对于b∈R都成立;
②当1<x≤2时,f(x)>0在[1,2]内恒成立?3b<
| x3 |
| x-1 |
| x3 |
| x-1 |
令g(x)=
| x3 |
| x-1 |
2x2(x-
| ||
| (x-1)2 |
| 3 |
| 2 |
列表如下:

由表格可知:当x=
| 3 |
| 2 |
| 3 |
| 2 |
(
| ||
|
| 27 |
| 4 |
∴3b<
| 27 |
| 4 |
| 9 |
| 4 |
综上①②可知:b的取值范围是(-∞,
| 9 |
| 4 |
点评:熟练掌握利用导数研究函数的单调性、极值与最值、分类讨论的思想方法、恒成立问题的等价转化是解题的关键.

练习册系列答案
相关题目
 ,请你根据上面探究结果,解答以下问题
,请你根据上面探究结果,解答以下问题 x3-
x3- x2+3x-
x2+3x-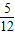 的对称中心为 ;
的对称中心为 ; +…+f(
+…+f(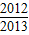 )= .
)= .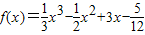 ,请你根据上面探究结果,解答以下问题
,请你根据上面探究结果,解答以下问题 x3-
x3- x2+3x-
x2+3x-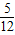 的对称中心为 ;
的对称中心为 ;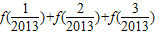 +…+f(
+…+f(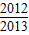 )= .
)= .