题目内容
(本小题满分14分)已知椭圆 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
⑴求椭圆C的方程;
⑵设 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 于另一点
于另一点 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线 与
与 轴相交于定点.
轴相交于定点.
 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.⑴求椭圆C的方程;
⑵设
 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 于另一点
于另一点 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;⑶在⑵的条件下,证明直线
 与
与 轴相交于定点.
轴相交于定点.解:⑴由题意知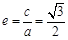 ,所以
,所以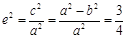 ,即
,即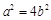 ,又因为
,又因为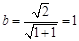 ,所以
,所以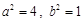 ,故椭圆
,故椭圆 的方程为
的方程为 :
: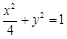 .
.
⑵由题意知直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为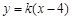 ①
①
联立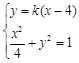 消去
消去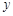 得:
得: ,
,
由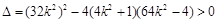 得
得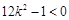 ,
,
又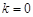 不合题意,
不合题意,
所以直线 的斜率的取值范围是
的斜率的取值范围是 或
或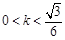 .
.
⑶设点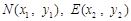 ,则
,则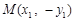 ,直线
,直线 的方程为
的方程为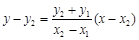 ,
,
令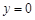 ,得
,得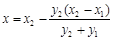 ,将
,将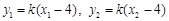 代入整理,得
代入整理,得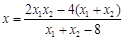 . ②由得①
. ②由得①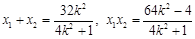 代入②整理,得
代入②整理,得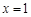 ,
,
所以直线 与
与 轴相交于定点
轴相交于定点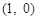 .
.
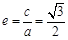 ,所以
,所以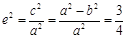 ,即
,即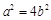 ,又因为
,又因为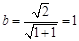 ,所以
,所以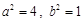 ,故椭圆
,故椭圆 的方程为
的方程为 :
: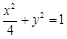 .
.⑵由题意知直线
 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为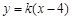 ①
①联立
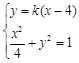 消去
消去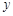 得:
得: ,
,由
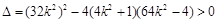 得
得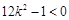 ,
,又
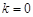 不合题意,
不合题意,所以直线
 的斜率的取值范围是
的斜率的取值范围是 或
或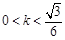 .
.⑶设点
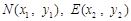 ,则
,则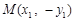 ,直线
,直线 的方程为
的方程为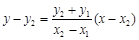 ,
,令
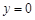 ,得
,得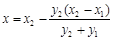 ,将
,将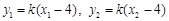 代入整理,得
代入整理,得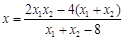 . ②由得①
. ②由得①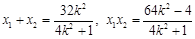 代入②整理,得
代入②整理,得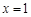 ,
,所以直线
 与
与 轴相交于定点
轴相交于定点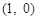 .
.略

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
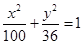 上一点P到焦点
上一点P到焦点 的距离等于6,那么点P到另一个焦点
的距离等于6,那么点P到另一个焦点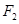 的距离是
的距离是 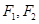 分别为椭圆
分别为椭圆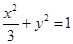 的左、右焦点,点
的左、右焦点,点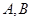 在椭圆上,若
在椭圆上,若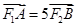 ;则点
;则点 的坐标是 ______.
的坐标是 ______.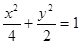 的左右焦点分别为
的左右焦点分别为 ,过
,过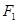 且倾角为
且倾角为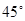 的直线
的直线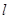 交椭圆于
交椭圆于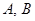 两点,对以下结论:①
两点,对以下结论:①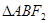 的周长为
的周长为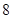 ;②原点到
;②原点到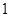 ;③
;③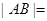
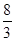 ;其中正确的结论有几个
;其中正确的结论有几个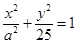 (
(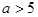 ),它的焦点分别为
),它的焦点分别为 ,
,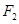 且︱
且︱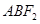 的周长为 ( )
的周长为 ( )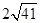 D
D 
 为圆
为圆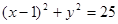 的弦
的弦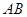 的中点,则直线
的中点,则直线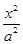 +
+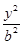 =1(a>b>0)经过点A
=1(a>b>0)经过点A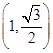 ,且离心率e=
,且离心率e=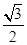 .
. O.若存在,求出直线l的方程;若不存在,说明理由.
O.若存在,求出直线l的方程;若不存在,说明理由. 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有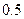 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽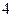 米,车高
米,车高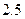 米.
米.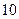 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行? 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?