Question

【题目】如图，在平面直角坐标系xOy中，焦点在x轴上的椭圆C： 经过点(b，2e)，其中e为椭圆C的离心率．过点T(1，0)作斜率为k(k＞0)的直线l交椭圆C于A，B两点(A在x轴下方)．

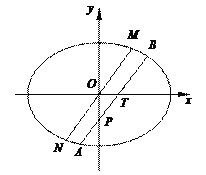
（1）求椭圆C的标准方程；

（2）过点O且平行于l的直线交椭圆C于点M，N，求 的值；

（3）记直线l与y轴的交点为P．若，求直线l的斜率k．

Answer 1

【答案】（1）;（2）;（3）

【解析】试题分析：（1）根据题意，把点代入椭圆的方程和，列出方程组，求解的值，即可得到椭圆的方程；

（2）设，直线的方程为，联立方程组，利用根与系数的关系，写出韦达定理，又由，得的方程为，联立方程组，求得点的坐标，即可求解结论；

（3）由直线，得，求得的坐标，再根据，得到，由（2）中的韦达定理，得出关于的方程，即可求解结论。

试题解析：

（1）因为椭圆＋＝1经过点(b，2e)，所以＋＝1．

因为e2＝＝，所以＋1．

因为a2＝b2＋c2，所以＋＝1．

整理得 b4－12b2＋32＝0，解得b2＝4或b2＝8(舍) ．

所以椭圆C的方程为＋＝1．

（2）设A(x1，y1)，B(x2，y2)．因为T(1，0)，则直线l的方程为y＝k(x－1)．

联立直线l与椭圆方程

消去y，得 (2k2＋1)x2－4k2x＋2k2－8＝0，

所以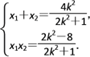

因为MN∥l，所以直线MN方程为y＝kx，

联立直线MN与椭圆方程

消去y得 (2k2＋1)x2＝8，解得x2＝．

因为MN∥l，所以＝．

因为 (1－x1)·(x2－1)＝－[x1x2－(x1＋x2)＋1]＝，

(xM－xN)2＝4x2＝，

所以＝＝·＝．

（3）在y＝k(x－1)中，令x＝0，则y＝－k，所以P(0，－k)，

从而＝(－x1,－k－y1)，＝(x2－1，/span>y2)．

因为＝，所以－x1＝ (x2－1)，即x1＋x2＝．由(2)知，

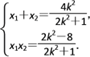
由解得 x1＝，x2＝．因为x1x2＝， 所以×＝，

整理得 50k4－83k2－34＝0，解得k2＝2或k2＝－(舍) ．

又因为k＞0，所以k＝．