题目内容
用数学归纳法证明1+
≤1+
+
+…+
≤
+n(n∈N*).
证明:(1)当n=1时,1+=,?
∴1+≤1+≤+1,?
即n=1时命题成立.?
(2)假设当n=k时命题成立,即1+
≤1+
+
+…+
≤
+k.?
则当n=k+1时,1+
+
+…+
+
+…+
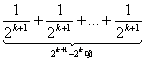≥1+
+
+…+
≥1+
+
=1+
+
=1+
.?
又1+
+
+…+
+
+…+
≤
+k+
＜
+(k+1).?
∴1+
≤1+
+
+…+
≤
+(k+1),即n=k+1时命题成立.?
由(1)(2)知,n∈N*时,原命题成立.
练习册系列答案
相关题目
用数学归纳法证明1+2+3+…+n2=
，则当n=k+1时左端应在n=k的基础上加上（ ）
| n4+n2 |
| 2 |
| A、k2+1 | ||
| B、（k+1）2 | ||
C、
| ||
| D、（k2+1）+（k2+2）+（k2+3）+…+（k+1）2 |
用数学归纳法证明1+
+
+…+
＜n（n∈N+，n＞1）时，第一步应验证不等式（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
A、1+
| ||||||
B、1+
| ||||||
C、1+
| ||||||
D、1+
|