题目内容
若关于x的方程x2-x+a=0和x2-x+b=0（a≠b）的四个根可组成首项为
的等差数列，则a+b的值是
- A.
- B.
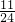
- C.
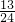
- D.
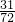
D
分析：先根据韦达定理确定a1+a2+a3+a4=1+1=2，再结合等差数列的性质可得到a1+a4=a2+a3=1，进而可求得a4和d，以及a2、a3的值，从而由a+b=a1a4+a2a3可确定答案．
解答：依题意设四根分别为a1、a2、a3、a4，公差为d，其中a1=，即a1+a2+a3+a4=1+1=2．又a1+a4=a2+a3，
所以a1+a4=a2+a3=1．
由此求得a4=
，d=
，
于是a2=
，a3=
．
故a+b=a1a4+a2a3=×+×=
=．
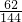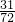故选D
点评：本题主要考查等差数列的性质和韦达定理的应用．考查基础知识的综合运用和计算能力．
分析：先根据韦达定理确定a1+a2+a3+a4=1+1=2，再结合等差数列的性质可得到a1+a4=a2+a3=1，进而可求得a4和d，以及a2、a3的值，从而由a+b=a1a4+a2a3可确定答案．
解答：依题意设四根分别为a1、a2、a3、a4，公差为d，其中a1=
，即a1+a2+a3+a4=1+1=2．又a1+a4=a2+a3，所以a1+a4=a2+a3=1．
由此求得a4=
，d=，于是a2=
，a3=．故a+b=a1a4+a2a3=
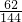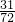×+×==．故选D
点评：本题主要考查等差数列的性质和韦达定理的应用．考查基础知识的综合运用和计算能力．
练习册系列答案
相关题目
△ABC中三个内角为A、B、C，若关于x的方程x2-xcosAcosB-cos2
=0有一根为1，则△ABC一定是（ ）
| C |
| 2 |
| A、直角三角形 |
| B、等腰三角形 |
| C、锐角三角形 |
| D、钝角三角形 |