题目内容
14．执行如图的程序框图，若输入x=12，则输出y=（ ）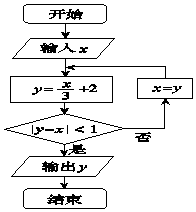
| A． | $\frac{10}{3}$ | B． | $\frac{5}{3}$ | C． | $\frac{3}{10}$ | D． | $\frac{3}{5}$ |
分析 由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量y的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
解答 解：模拟执行程序框图，可得
x=12，y=6，
不满足条件|y-x|＜1，x=6，y=4
不满足条件|y-x|＜1，x=4，y=$\frac{10}{3}$
由于|$\frac{10}{3}$|＜1，故此时满足条件|y-x|＜1，退出循环，输出y的值为$\frac{10}{3}$．
故选：A．
点评 本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．
练习册系列答案
相关题目
5．从集合A={-2，1，2}中随机选取一个数记为a，从集合B={-2，1，2}中随机选取一个数记为b，则直线bx-y+a=0不经过第四象限的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{2}{9}$ | D． | $\frac{4}{9}$ |
2．阅读如图的程序框图，若输出S=30，则在判断框 内应填入（ ）
| A． | i＞5 | B． | i＞6 | C． | i＞4 | D． | i≥4 |
19．
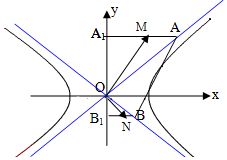如图，A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$两渐近线上的点，A、B在y轴上的射影分别为A1、B1，M、N分别是A1A、B1B、的中点，若AB中点在双曲线上，且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$，则双曲线的离心率的取值范围为（ ）
如图，A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$两渐近线上的点，A、B在y轴上的射影分别为A1、B1，M、N分别是A1A、B1B、的中点，若AB中点在双曲线上，且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$，则双曲线的离心率的取值范围为（ ）| A． | $（{1，\frac{3}{2}}]$ | B． | $[\frac{3}{2}，+∞）$ | C． | $（1，\frac{{\sqrt{5}}}{2}]$ | D． | $[\frac{{\sqrt{5}}}{2}，+∞）$ |
