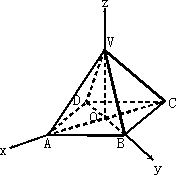
题目内容
已知正四棱锥O-ABCD的体积为
，底面边长为
，则以O为球心，OA为半径的球的表面积为
3
| ||
| 2 |
| 3 |
24π
24π
．分析：先直接利用锥体的体积公式即可求得正四棱锥O-ABCD的高，再利用直角三角形求出正四棱锥O-ABCD的侧棱长OA，最后根据球的表面积公式计算即得．
解答：
解：如图，正四棱锥O-ABCD的体积V=
sh=
（
×
）×OH=
，
∴OH=
，
在直角三角形OAH中，OA=
=
=
所以表面积为4πr2=24π；
故答案为：24π．
解：如图，正四棱锥O-ABCD的体积V=| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
3
| ||
| 2 |
∴OH=
3
| ||
| 2 |
在直角三角形OAH中，OA=
| AH2+OH2 |
(
|
| 6 |
所以表面积为4πr2=24π；
故答案为：24π．
点评：本题考查锥体的体积、球的表面积计算，考查学生的运算能力，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
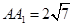，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，则有以下结论：
[]
；
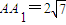，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，有以下判断，
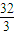；（3）存在过点E的平面，截球O的截面面积是3π；（4）三棱锥P-AEC1体积的最大值是20．