题目内容

精英家教网如图，四面体ABCD中，点E是CD的中点，记
AB
=
a
，
AC
=
b
，
AD
=
c
，则
BE
=（　　）
A、
a
-
1
2
b
+
1
2
c
B、-
a
+
1
2
b
+
1
2
c
C、
1
2
a
-
b
+
1
2
c
D、-
1
2
a
+
b
+
1
2
c
分析：连接AE，根据AE是△ACD中CD边上的中线，可得向量
AE
是
AC
、
AD
和的一半，再在△ABE中利用向量加法的三角形法则，即可得到向量
BE
关于向量
a
、
b
、
c
的表达式．
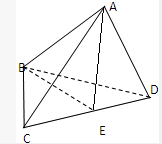
解答：解：连接AE，精英家教网
∵E是CD的中点，
AC
=
b
，
AD
=
c

∴
AE
=
1
2
(
AC
+
AD
)=
1
2
(
b
+
c
)
∵△ABE中，
BE
=
BA
+
AE
=-
AB
+
AE
，
AB
=
a

∴
BE
=-
a
+
1
2
(
b
+
c
)=-
a
+
1
2
b
+
1
2
c

故选：B
点评：本题在四面体ABCD中，已知E为CD中点的情况下求向量
AE
的表达式，着重考查了向量的加法法则、空间向量的线性运算的知识，属于基础题．
练习册系列答案
相关题目
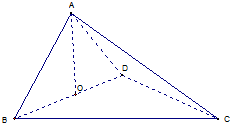精英家教网如图，四面体ABCD中，O是BD的中点，△ABD和△BCD均为等边三角形，
AB=2，AC=
6
．
（I）求证：AO⊥平面BCD；
（II）求二面角A-BC-D的大小；
（III）求O点到平面ACD的距离．
如图，四面体ABCD中，O．E分别为BD．BC的中点，且CA=CB=CD=BD=2，AB=AD=
2
．
（1）求证：AO⊥平面BCD；
（2）求 异面直线AB与CD所成角的余弦值．
如图，四面体ABCD中，0是BD的中点，CA=CB=CD=BD=a，AB=AD=
2
2
a．
（1）求证：平面AOC⊥平面BCD；
（2）求二面角O-AC-D的余弦值．
如图，四面体ABCD的各个面都是直角三角形，已知AB⊥BC，BC⊥CD，AB=a，BC=a，CD=c．
（1）若AC⊥CD，求证：AB⊥BD；
（2）求四面体ABCD的表面积．
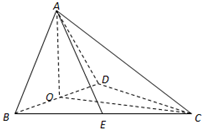精英家教网如图，四面体ABCD中，O、E分别是BD、BC的中点，AO⊥平面BCD，CA=CB=CD=BD=2．
（1）求证：面ABD⊥面AOC；
（2）求异面直线AE与CD所成角的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网