题目内容

将函数y=sin(2x+
π
3
)的图象沿坐标轴右移，使图象的对称轴与函数y=cos(2x+
π
3
)的对称轴重合，则平移的最小单位是______．
函数 y=cos(2x+
π
3
)的图象的对称轴为：2x+
π
3
=k′π，
即x=
k′π
2
-
π
6
，k′∈Z；
函数y=sin(2x+
π
3
)的图象沿坐标轴向右平移φ个单位，
得到y=sin(2x-2φ+
π
3
)的图象，
函数y=sin(2x-2φ+
π
3
)的对称轴为：2x-2φ+
π
3
=kπ+
π
2
，
即：x=φ+
π
6
+
kπ
2
 k∈Z，
由于对称轴相同，
k′π
2
-
π
6
=φ+
π
12
+
kπ
2
，φ＞0
∴当k′=1，k=0时，
所以φ的最小值为
π
4
．
故答案为：
π
4
练习册系列答案
相关题目
给出下列命题：
①在△ABC中，若A＜B，则sinA＜sinB；
②将函数y=sin(2图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
③在△ABC中，若AB=2，AC=3，∠ABC=60°，则△ABC必为锐角三角形；
④在同一坐标系中，函数y=sinx的图象和函数y=
x
2
的图象有三个公共点．
其中真命题是
 
．（填出所有正确命题的序号）
将函数y=sin(6x+
π
4
)的图象上各点的横坐标伸长到原来的3倍，再向右平移
π
8
个单位，得到的函数的一个对称中心（　　）
将函数y=sin(x+
π
3
)的图象向右平移
π
6
个单位，再向上平移2个单位所得图象对应的函数解析式是
y=sin(x+
π
6
)+2
y=sin(x+
π
6
)+2
．
将函数y=sin(
1
2
x+
π
3
)的图象作如下那种变换，才能得到函数y=sin(
1
2
x)的图象（　　）

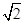要得到函数y=cos(2+)的图象, 只需要将函数y=sin(2+)图象上所有的点(     )

A．向左平移个单位，纵坐标不变；

B．向右平移个单位，纵坐标不变；

C．向左平移个单位，纵坐标不变；

D．向右平移 个单位，纵坐标不变．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网