Question

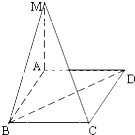正方形ABCD的边长为a，MA⊥平面ABCD，且MA=a，则点D到平面MBC的距离为

2 a

2

．

Answer 1

分析：取MB的中点E并连结EA，利用线面垂直的判定与性质，结合题意证出AE⊥平面MBC．再由线面平行判定定理，证出AD∥平面MBC，可得点D到平面MBC的距离等于A到平面MBC的距离，由此可得点D到平面MBC的距离．

解答：解：取MB的中点E，连结EA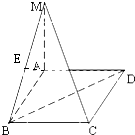
∵MA⊥平面ABCD，BC?平面ABCD，∴BC⊥MA
∵正方形ABCD中，BC⊥AB，且MA∩AB=A
∴BC⊥平面MAB，
∵AE?平面MAB，∴AE⊥BC
又∵△MAB中，MA=AB=a，∠MAB=90°，
∴AE⊥MB，且AE=

2 a

2

∵BC、MB是平面MBC内的相交直线，
∴AE⊥平面MBC
∵AD∥BC，AD?平面MBC，BC?平面MBC，
∴AD∥平面MBC，可得点D到平面MBC的距离等于A到平面MBC的距离
即点D到平面MBC的距离等于AE=

2 a

2

故答案为：

2 a

2

点评：本题求点到平面的距离，着重考查了线面垂直的判定与性质、线面平行判定定理和空间点到平面距离的定义与求法等知识，属于中档题．