Question

计算下列各式的值:

(1)

(2)

(3)求(1-i)¹⁰的展开式中的所有奇数项的和.

Answer 1

分析：对于以上三例若按复数乘除法和乘方法直接计算,则显得十分繁锁.若能结合题目特点,联想结论(1±i)²=±2i和ω的性质,对于(2)题并注意到-2+i=i(1+2i),对于(3)利用二项式定理展开,不难找出简捷解法.

解：(1)原式=

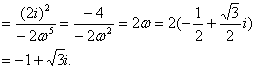
其中ω=-+i.

(2)原式=

=i+()^{1 003}

=i+i^{1 003}=i+i^4×250+3=i+i³=i-i=0.

(3)∵(1-i)¹⁰=1-·i+·(i)²-·(i)³+…,

∴(1-i)¹⁰的展开式中奇数项之和为复数(1-3i)¹⁰的实部.

又(1-i)¹⁰=［-2·(-+i)］¹⁰=2¹⁰ω¹⁰=2¹⁰ω=2¹⁰(-+i)=-2⁹+2⁹i.

∴(1-i)¹⁰的展开式中各奇数项的和为-2⁹.

点评 代数形式的复数运算,基本思路是应用法则,但如果能通过对表达式的结构特征进行分析,灵活运用i的幂的性质、1的立方虚根ω的性质以及1±i的幂的性质等,将可有效地简化运算,提高效率.