题目内容
（2012•开封一模）已知双曲线
-
=1(a＞0，b＞0)的渐近线到点M（3，0）的距离为2，则双曲线的离心率为
．
| x2 |
| a2 |
| y2 |
| b2 |
3
| ||
| 5 |
3
| ||
| 5 |
分析：根据双曲线
-
=1(a＞0，b＞0)的渐近线到点M（3，0）的距离为2，可得
=2，由此可求双曲线的离心率．
| x2 |
| a2 |
| y2 |
| b2 |
| 3b | ||
|
解答：解：双曲线
-
=1(a＞0，b＞0)的渐近线方程为
±
=0，即bx±ay=0
∵渐近线到点M（3，0）的距离为2，
∴
=2
∴a2=
b2
∴e2=
=
∴e=
故答案为：
| x2 |
| a2 |
| y2 |
| b2 |
| x |
| a |
| y |
| b |
∵渐近线到点M（3，0）的距离为2，
∴
| 3b | ||
|
∴a2=
| 5 |
| 4 |
∴e2=
| a2+b2 |
| a2 |
| 9 |
| 5 |
∴e=
3
| ||
| 5 |
故答案为：
3
| ||
| 5 |
点评：本题考查双曲线的几何性质，考查点到直线的距离公式的运用，确定双曲线的渐近线方程是关键．
练习册系列答案
相关题目
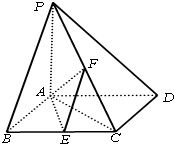（2012•开封一模）已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．