题目内容
已知向量 ,
, ,且α+β=4.
,且α+β=4.
(1)求 ,
, 的夹角θ的大小;
的夹角θ的大小;
(2)求 的最小值.
的最小值.
解:(1) ,
,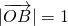

 .
.
当λ>0时,cosθ=sin4=cos(4- ),
),
因0≤θ≤π, ,故
,故 ;
;
当λ<0时, ,
,
因0≤θ≤π, ,故
,故
(2)
=
=λ2-2λsin(α+β)+1
=λ2-2λsin4+cos24+sin24
=(λ-sin4)2+cos24
≥cos24
所以 的最小值为-cos4.
的最小值为-cos4.
分析:(1)利用向量的数量积表示出向量的夹角余弦,据向量夹角的范围对λ分类讨论求出角θ
(2)利用向量模的平方等于向量的平方表示出模,利用二次函数的最值的求法求出模的最小值.
点评:本题考查利用向量的数量积求向量的夹角;向量模的平方等于向量的平方;二次函数最值的求法.
 ,
,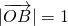

 .
.当λ>0时,cosθ=sin4=cos(4-
 ),
),因0≤θ≤π,
 ,故
,故 ;
;当λ<0时,
 ,
,因0≤θ≤π,
 ,故
,故
(2)

=

=λ2-2λsin(α+β)+1
=λ2-2λsin4+cos24+sin24
=(λ-sin4)2+cos24
≥cos24
所以
 的最小值为-cos4.
的最小值为-cos4.分析:(1)利用向量的数量积表示出向量的夹角余弦,据向量夹角的范围对λ分类讨论求出角θ
(2)利用向量模的平方等于向量的平方表示出模,利用二次函数的最值的求法求出模的最小值.
点评:本题考查利用向量的数量积求向量的夹角;向量模的平方等于向量的平方;二次函数最值的求法.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
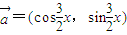 ,
,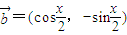 .且x
.且x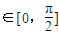
 ;
;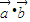 -2λ|
-2λ|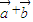 |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值. ,
, ,且
,且 与
与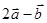 互相垂直,则k等于
_______________________(用分数作答)
互相垂直,则k等于
_______________________(用分数作答) 满足
满足 ,且
,且 ,则
,则 的夹角为( )
的夹角为( ) B、
B、 C、
C、 D、
D、
 满足
满足 ,且
,且 ,则
,则 等于( ▲ )
等于( ▲ ) B.
B. C.
C. D.7
D.7