题目内容
已知函数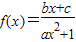 (a,b,c∈R,a>0)是奇函数,若f(x)的最小值为
(a,b,c∈R,a>0)是奇函数,若f(x)的最小值为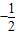 ,且
,且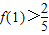 ,则b的取值范围是 .
,则b的取值范围是 .
【答案】分析:已知f(x)为奇函数可得f(-x)=-f(x),其中f(0)=0,解出c=0,对f(x)进行变形利用均值不等式得出f(x)的最小值,再根据f(x)的最小值为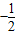 ,求出a与b的关系式,代入
,求出a与b的关系式,代入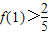 得b的范围;
得b的范围;
解答:解:∵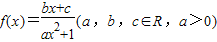 ,是奇函数,
,是奇函数,
∴f(0)=0,
∴c=0,
∵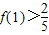 >0,
>0,
∴b>0,
∴f(x)=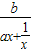 ≥
≥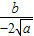 ,
,
∴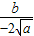 =-
=- ,
,
∴a=b2,解得f(1)=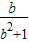 >
> 得
得 <b<2,
<b<2,
故答案为: <b<2.
<b<2.
点评:此题主要考查函数的奇偶性,以及利用均值不等式的来求未知量的范围,是一道中档题;
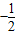 ,求出a与b的关系式,代入
,求出a与b的关系式,代入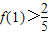 得b的范围;
得b的范围;解答:解:∵
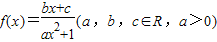 ,是奇函数,
,是奇函数,∴f(0)=0,
∴c=0,
∵
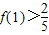 >0,
>0,∴b>0,
∴f(x)=
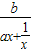 ≥
≥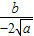 ,
,∴
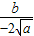 =-
=- ,
,∴a=b2,解得f(1)=
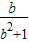 >
> 得
得 <b<2,
<b<2,故答案为:
 <b<2.
<b<2.点评:此题主要考查函数的奇偶性,以及利用均值不等式的来求未知量的范围,是一道中档题;

练习册系列答案
相关题目
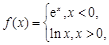 则
则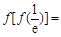 ( )
( )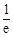 B.
B.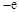 C.
C.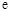 D.
D. (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3,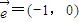 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称.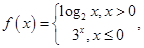 则
则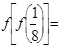 ( )
( )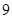 B.
B.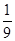 C.
C.
 D.
D.
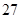
 已知函数
已知函数  若
若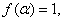
 =
=