题目内容
设非零向量 、
、 、
、 满足
满足 ,
,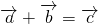 ,则向量
,则向量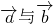 的夹角为
的夹角为
- A.30°
- B.60°
- C.120°
- D.150°
C
分析:设向量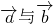 的夹角为θ,由题意可得
的夹角为θ,由题意可得 =
=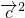 ,由此求得cosθ 的值,再由θ的范围,求得 θ的值.
,由此求得cosθ 的值,再由θ的范围,求得 θ的值.
解答:设向量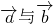 的夹角为θ,
的夹角为θ,
∵非零向量 、
、 、
、 满足
满足 ,
,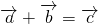 ,
,
∴ =
=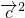 ,即
,即 =
=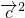 ,
,
即 =
= .
.
解得 cosθ=- ,再由 0°≤θ≤180°,可得 θ=120°,
,再由 0°≤θ≤180°,可得 θ=120°,
即向量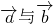 的夹角为 120°,
的夹角为 120°,
故选C.
点评:本题主要考查两个向量的夹角公式,两个向量数量积公式,根据三角函数的值求角,属于中档题.
分析:设向量
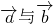 的夹角为θ,由题意可得
的夹角为θ,由题意可得 =
=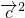 ,由此求得cosθ 的值,再由θ的范围,求得 θ的值.
,由此求得cosθ 的值,再由θ的范围,求得 θ的值.解答:设向量
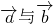 的夹角为θ,
的夹角为θ,∵非零向量
 、
、 、
、 满足
满足 ,
,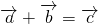 ,
,∴
 =
=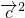 ,即
,即 =
=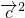 ,
,即
 =
= .
.解得 cosθ=-
 ,再由 0°≤θ≤180°,可得 θ=120°,
,再由 0°≤θ≤180°,可得 θ=120°,即向量
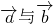 的夹角为 120°,
的夹角为 120°,故选C.
点评:本题主要考查两个向量的夹角公式,两个向量数量积公式,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
 、
、 、
、 满足
满足 ,则
,则
 、
、 、
、 满足
满足 ,则
,则 ( )
( ) 、
、 、
、 满足
满足 ,则
,则