Question

【题目】经市场调查，某旅游城市在过去的一个月内（以30天计），第t天（1≤t≤30，t∈N*）的旅游人数f（t）（单位：万人）近似地满足f（t）=4+ ，而人均日消费俄g（t）（单位：元）近似地满足g（t）= ．
（1）试求所有游客在该城市旅游的日消费总额W（t）（单位：万元）与时间t（1≤t≤30，t∈N*）的函数表达式；
（2）求所有游客在该城市旅游的日消费总额的最小值．

Answer 1

【答案】
（1）解：由题意，根据该城市的旅游日消费总额=日旅游人数×人均消费的钱数，

可得：W（t）=f（t）g（t）

= ；

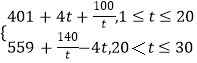（2）解：由（1）可知：当t∈[1，20]时，401+4t+ ≥401+2 =441，

当且仅当4t= 即t=5时取等号；

当t∈（20，30]时，因为W（t）=559+ ﹣4t递减，

所以t=30时，W（t）有最小值W（30）=443+ ，

∵443+ ＞441，

∴t∈[1，30]时，W（t）的最小值为441万元．

【解析】（1）利用日消费总额=日旅游人数×人均消费的钱数，化简即得结论；（2）通过（1）可知当t∈[1，20]时利用基本不等式可知当且仅当t=5时取最小值441，当t∈（20，30]时利用函数的单调性可知当t=30时W（t）有最小值443+ ，进而比较即得结论．