题目内容
(本小题满分12分)已知函数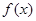 满足
满足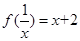 .
.
(Ⅰ)求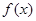 的解析式及其定义域;
的解析式及其定义域;
(Ⅱ)写出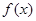 的单调区间并证明.
的单调区间并证明.
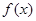 满足
满足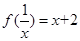 .
.(Ⅰ)求
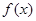 的解析式及其定义域;
的解析式及其定义域;(Ⅱ)写出
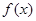 的单调区间并证明.
的单调区间并证明.(Ⅰ)
(Ⅱ)函数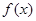 在区间
在区间 单调递减,用函数单调性的定义证明即可.
单调递减,用函数单调性的定义证明即可.

(Ⅱ)函数
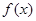 在区间
在区间 单调递减,用函数单调性的定义证明即可.
单调递减,用函数单调性的定义证明即可.试题分析:(Ⅰ)令
 , ……2分
, ……2分则
 , ……4分
, ……4分∴
 ,
,∴
 . ……6分
. ……6分(Ⅱ)函数
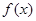 在区间
在区间 单调递减. ……7分
单调递减. ……7分设
 ,
, , ……8分
, ……8分 , ------10分
, ------10分当
 时,
时, ∴
∴ ;
;同理,当
 时,
时, ,
,∴函数
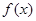 在区间
在区间 单调递减. ……12分
单调递减. ……12分点评:换元法求函数的解析式时,要注意换元前后自变量的取值范围是否发生了变化;利用定义证明函数的单调性时,要严格按照取值——作差——变形——判号——结论几个步骤进行,变形要变的彻底.

练习册系列答案
相关题目
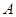 、
、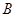 两个项目,预计投资
两个项目,预计投资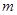 万元可获得利润
万元可获得利润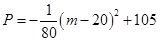
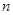 万元可获得利润
万元可获得利润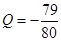
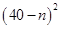
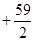
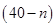 万元.若该企业用40
万元.若该企业用40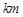 的A,B两家工厂(视作污染源)的污染强度分别为
的A,B两家工厂(视作污染源)的污染强度分别为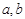 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两家工厂对该处的污染指数之和.设
等于两家工厂对该处的污染指数之和.设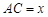 (
(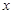 的函数;
的函数;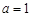 ,且
,且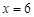 时,
时,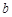 的值.
的值.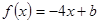 ,且不等式
,且不等式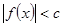 的解集为
的解集为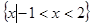 ,
,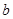 的值;
的值; 的不等式
的不等式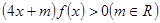
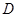 的函数
的函数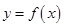 和常数
和常数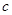 ,若对任意正实数
,若对任意正实数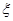 ,
,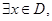 使得
使得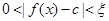 恒成立,则称函数
恒成立,则称函数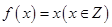 ; ②
; ②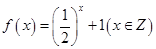 ;
;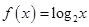 ; ④
; ④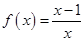 .
.  ,B=R,映射
,B=R,映射 ,对应法则为
,对应法则为 ,对于实数
,对于实数 ,在集合A中不存在原象,则实数
,在集合A中不存在原象,则实数 的取值范围是
的取值范围是



 (万元)和
(万元)和 (万元),它们与投入的资金
(万元),它们与投入的资金 (万元)的关系,据经验估计为:
(万元)的关系,据经验估计为: ,
,  今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?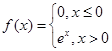 ,则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是
,则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是

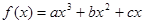 是
是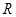 上的奇函数,且
上的奇函数,且
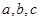 的值
的值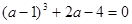 ,
,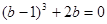 ,求
,求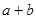 的值
的值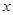 的不等式
的不等式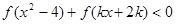 在
在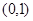 上恒成立,求
上恒成立,求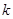 的取值范围
的取值范围