题目内容
下列说法错误的是
- A.命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1则x2-3x+2≠0”
- B.命题p:“?x∈R,使得x2+x+1<0”,则?p:“?x∈R,均有x2+x+1≥0”
- C.若“p且q”为假命题,则p,q至少有一个为假命题
- D.若
 是“
是“ ”的充要条件
”的充要条件
D
分析:根据逆否命题是对命题的条件、结论分别进行否定且交换条件与结论可判断;
根据特称命题的否定是全称命题可判断B
根据复合命题的真假关系可知,当“p且q”为假命题,则p,q至少有一个为假命题,
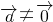 ,若
,若 时,不一定有
时,不一定有 ,
,
解答:根据逆否命题是对命题的条件、结论分别进行否定且交换条件与结论可知A正确
根据特称命题的否定是全称命题可知B正确
根据复合命题的真假关系可知,当“p且q”为假命题,则p,q至少有一个为假命题,故C正确
若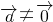 ,则
,则 时,有
时,有 ,但是若
,但是若 时,不一定有
时,不一定有 ,故D错误
,故D错误
故选D
点评:本题主要考查了四种命题的关系,全称命题与特称命题的关系及复合命题的真假关系及向量的数量积的性质的简单应用
分析:根据逆否命题是对命题的条件、结论分别进行否定且交换条件与结论可判断;
根据特称命题的否定是全称命题可判断B
根据复合命题的真假关系可知,当“p且q”为假命题,则p,q至少有一个为假命题,
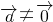 ,若
,若 时,不一定有
时,不一定有 ,
,解答:根据逆否命题是对命题的条件、结论分别进行否定且交换条件与结论可知A正确
根据特称命题的否定是全称命题可知B正确
根据复合命题的真假关系可知,当“p且q”为假命题,则p,q至少有一个为假命题,故C正确
若
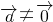 ,则
,则 时,有
时,有 ,但是若
,但是若 时,不一定有
时,不一定有 ,故D错误
,故D错误故选D
点评:本题主要考查了四种命题的关系,全称命题与特称命题的关系及复合命题的真假关系及向量的数量积的性质的简单应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f:A→B是从集合A到B的映射,下列说法错误的是
A.A中的每一个元素在B中必有象
B.B中可能有元素在A中没有原象
C.A中两个不同的元素在B中的象一定不相同
D.B中的某个元素在A中的原象可能不只一个
下列说法错误的是 ( )
A.命题“若 ,则 ,则 ”的逆否命题为:“若 ”的逆否命题为:“若 ,则 ,则 ”. ”. |
B.“ ”是“ ”是“ ”的充分不必要条件. ”的充分不必要条件. |
C.若 且 且 为假命题,则 为假命题,则 、 、 均为假命题. 均为假命题. |
D.命题 :存在 :存在 使得 使得 . 则 . 则 :任意 :任意 ,均有 ,均有 . . |
 是
是 或
或 的充分不必要条件
的充分不必要条件
 ,则
,则

 的绝对值越接近
的绝对值越接近 ,表示两变量的相关性越强.
,表示两变量的相关性越强.