题目内容
19.某卫生机构对366人进行健康体检,其中某项检测指标阳性家族史者糖尿病发病的有16人,不发病的有93人;阴性家族史者糖尿病发病的有17人,不发病的有240人,(1)有多少的把握认为糖尿病患者与遗传有关系?
(2)那么这种判断出错的可能性为多少?
分析 (1)通过所给的数据计算K2观测值,同临界值表中的数据进行比较,可得到结论.
(2)由(1)中结论,可得这种判断出错的可能性.
解答 解:(1)可以先作出如下列联表(单位:人):
糖尿病患者与遗传列联表
| 糖尿病发病 | 糖尿病不发病 | 总计 | |
| 阳性家族史 | 16 | 93 | 109 |
| 阴性家族史 | 17 | 240 | 257 |
| 总计 | 33 | 333 | 366 |
K2=$\frac{366×{(16×240-17×93)}^{2}}{109×257×33×333}$≈6.067>5.024.
故我们有97.5%的把握认为糖尿病患者与遗传有关系
(2)出错的可能性为2.5%
点评 本题考查独立性检验,考查判断两个变量之间有没有关系,一般题目需要自己做出观测值,再拿着观测值同临界值进行比较,得到结论,本题给出了观测值,只剩下一个比较过程.

练习册系列答案
相关题目
9.已知关于x的方程4x2-2(m+1)x+m=0的两个根恰好是一个直角三角形的两个锐角的余弦值,实数m的值( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
14.若sin$\frac{α}{2}$=$\frac{1}{3}$,则cos(π+α)等于( )
| A. | -$\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | -$\frac{5}{9}$ | D. | $\frac{5}{9}$ |
11.已知x+x-1=3,则x2+x-2等于( )
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
9.已知f(x)是偶函数,它在[0,+∞)上是增函数,若f(lgx)>f(-1).则x的取值范围是( )
| A. | ($\frac{1}{10}$,1) | B. | (0,$\frac{1}{10}$)∪(10,+∞) | C. | ($\frac{1}{10}$,10) | D. | (0,1)∪(10,+∞) |
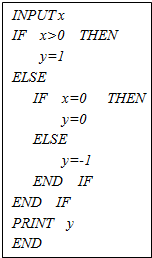 读程序,回答下列问题:
读程序,回答下列问题: