题目内容
数列{an}中,a1=2,an+1=an+cn(c是不为0的常数,n∈N*),且a1,a2,a3成等比数列.(1)求数列{an}的通项公式;
(2)若bn=
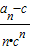 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】分析:(1)由已知可得,(2+c)2=2(2+3c)可求c,代入可得an+1=an+2n,利用叠加可求通项
(2)由bn=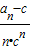 =
=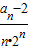 =
=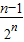 ,考虑利用错位相减可求和
,考虑利用错位相减可求和
解答:解:(1)由已知可知a2=2+c,a3=2+3c(1分)
则(2+c)2=2(2+3c)
∴c=2
从而有an+1=an+2n(2分)
当n≥2时,an=a1+(a2-a1)+a3-a2+…+(an-an-1)
=2+2×1+2×2+…+2n=n2-n+2(4分)
当n=1时,a1=2适合上式,因而an=n2-n+2(5分)
(2)∵bn=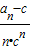 =
=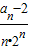 =
=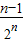 (6分)
(6分)
Tn=b1+b2+…+bn=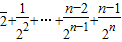
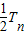 =
=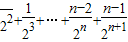
相减可得,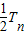 =
=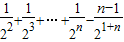 =
=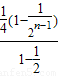
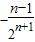 (9分)
(9分)
∴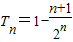 (10分)
(10分)
点评:本题主要考查了利用叠加法求解数列的通项公式,而错位相减求解数列的和是数列求和的重点和难点,要注意掌握
(2)由bn=
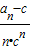 =
=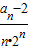 =
=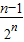 ,考虑利用错位相减可求和
,考虑利用错位相减可求和解答:解:(1)由已知可知a2=2+c,a3=2+3c(1分)
则(2+c)2=2(2+3c)
∴c=2
从而有an+1=an+2n(2分)
当n≥2时,an=a1+(a2-a1)+a3-a2+…+(an-an-1)
=2+2×1+2×2+…+2n=n2-n+2(4分)
当n=1时,a1=2适合上式,因而an=n2-n+2(5分)
(2)∵bn=
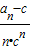 =
=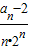 =
=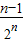 (6分)
(6分)Tn=b1+b2+…+bn=
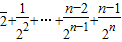
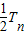 =
=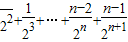
相减可得,
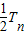 =
=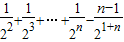 =
=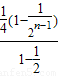
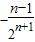 (9分)
(9分)∴
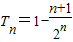 (10分)
(10分)点评:本题主要考查了利用叠加法求解数列的通项公式,而错位相减求解数列的和是数列求和的重点和难点,要注意掌握

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列{an}中,a1=
,an+an+1=
,n∈N*,则
(a1+a2+…+an)等于( )
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|