题目内容
已知: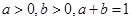 ,
,
(1)求证: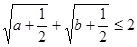 ; (2)求
; (2)求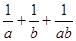 的最小值.
的最小值.
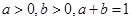 ,
,(1)求证:
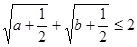 ; (2)求
; (2)求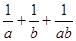 的最小值.
的最小值. (1) 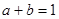 ,所以
,所以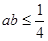 ,所以
,所以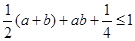 ,
,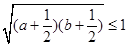 ,从而有2+
,从而有2+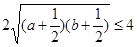 ,即:
,即: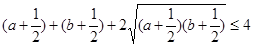 ,所以原不等式成立 (2)8
,所以原不等式成立 (2)8
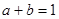 ,所以
,所以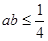 ,所以
,所以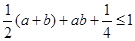 ,
,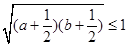 ,从而有2+
,从而有2+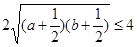 ,即:
,即: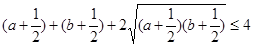 ,所以原不等式成立 (2)8
,所以原不等式成立 (2)8试题分析:(1)证明:因为
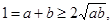 所以
所以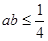 ,所以
,所以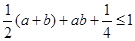
所以
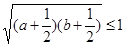 ,从而有2+
,从而有2+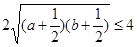
即:
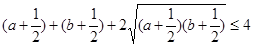
即:
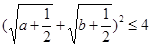 ,所以原不等式成立.
,所以原不等式成立. (2)
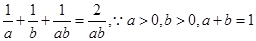 ……2分
……2分 即
即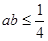 当且仅当
当且仅当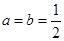 时等号成立
时等号成立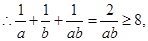 即当
即当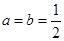 时,
时,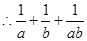 的最小值为8. 2分
的最小值为8. 2分点评:由均值不等式
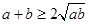 求最值时要满足一正二定三相等,一,
求最值时要满足一正二定三相等,一,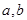 都是正实数,二,当和为定值时,积取最值,当积为定值时,和为定值,三,当且仅当
都是正实数,二,当和为定值时,积取最值,当积为定值时,和为定值,三,当且仅当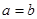 时等号成立取得最值
时等号成立取得最值
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
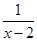 (x>2)在
(x>2)在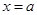 处取最小值,则
处取最小值,则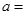
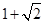
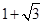
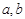 ,且
,且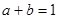 ,则
,则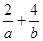 的最小值为 ( )
的最小值为 ( )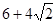
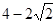
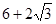
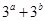 的最小值是( )
的最小值是( )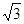
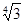
 成立的所有常数
成立的所有常数 中,我们把
中,我们把 叫做
叫做 的上确界,若
的上确界,若 ,则
,则 的上确界是( )
的上确界是( ) 



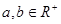 ,且
,且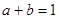 ,则
,则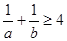 ;
;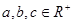 ,且
,且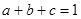 ,则
,则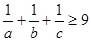 ;
;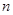 个正数
个正数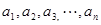 的结论?(写出结论,不必证明。
的结论?(写出结论,不必证明。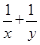 的最小值为 。
的最小值为 。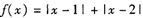 .
.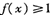 ;
;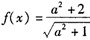 成立,求x的取值范围.
成立,求x的取值范围. 若
若 ,则
,则 最小值为
最小值为