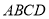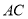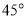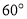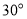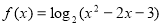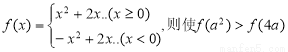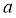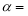题目内容
集合A是由适合以下性质的函数 构成的:对于定义域内任意两个不相等的实数
构成的:对于定义域内任意两个不相等的实数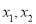 ,都有
,都有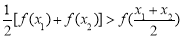 .
.
(1)试判断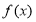 =
=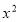 及
及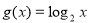 是否在集合A中,并说明理由;
是否在集合A中,并说明理由;
(2)设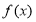 ?A且定义域为?0,??,值域为?0,1?,
?A且定义域为?0,??,值域为?0,1?,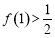 ,试写出一个满足以上条件的函数
,试写出一个满足以上条件的函数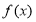 的解析式,并给予证明.
的解析式,并给予证明.
(1) ,
,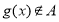 ;(2)
;(2)
【解析】
试题分析:(1)根据题目给出的性质对函数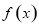 与
与 进行判断即可;(2)可以模仿(1)中的函数进行寻找,或者可以这么找,因为我们学了指数、对数、幂函数,而(1)中已经出现了对数函数与幂函数,所以是否可以考虑从指数函数中寻找.
进行判断即可;(2)可以模仿(1)中的函数进行寻找,或者可以这么找,因为我们学了指数、对数、幂函数,而(1)中已经出现了对数函数与幂函数,所以是否可以考虑从指数函数中寻找.
试题解析:(1) ,
,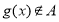 . 2分
. 2分
对于 的证明. 任意
的证明. 任意 且
且 ,
,
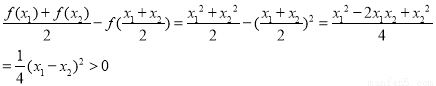
即 . ∴
. ∴ 4分
4分
对于 ,举反例:当
,举反例:当 ,
, 时,
时,
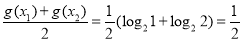 ,
,
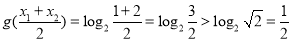 ,
,
不满足 . ∴
. ∴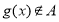 . 7分
. 7分
⑵函数 ,当
,当 时,值域为
时,值域为 且
且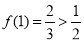 . 9分
. 9分
任取 且
且 ,则
,则

即 . ∴
. ∴ . 14分
. 14分
考点:1.函数性质;2.新定义型解答题;3.指数函数、对数函数、指数函数.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目