题目内容
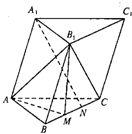 在斜三棱柱ABC-A1B1C1中,BB1=BA=BC=1,∠B1BC=60°,∠ABC=90°,平面BB1C1C⊥平面ABC,M、N分别是BC的三等分点.
在斜三棱柱ABC-A1B1C1中,BB1=BA=BC=1,∠B1BC=60°,∠ABC=90°,平面BB1C1C⊥平面ABC,M、N分别是BC的三等分点.(1)求证:A1N∥平面AB1M;
(2)求证:AB⊥B1M;
(3)求三棱锥A-B1BC的体积V.
分析:(1)OM为△A1BN的中位线,所以OM∥A1N又∵A1N?平面AB1M,OM?平面AB1M∴A1N∥平面AB1M.
(2)AB⊥BC,AB?平面ABC,所以AB⊥平面BB1C,又B1M?平面BB1C1C,∴AB⊥B1M.
(3)由AB⊥平面BB1C1C可得三棱锥的高是AB,底面为三角形BCB1所以可求的三棱锥的体积为
×(
× 1×1×sin60°)×1=
.
(2)AB⊥BC,AB?平面ABC,所以AB⊥平面BB1C,又B1M?平面BB1C1C,∴AB⊥B1M.
(3)由AB⊥平面BB1C1C可得三棱锥的高是AB,底面为三角形BCB1所以可求的三棱锥的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 12 |
解答:解(1)连A1B交AB1与O,连OM,
则OM为△A1BN的中位线
∴OM∥A1N
∵A1N?平面AB1M,OM?平面AB1M
∴A1N∥平面AB1M.
(2)∵平面BB1C1C⊥平面ABC,而∠ABC=90°
∴AB⊥BC,AB?平面ABC
∴AB⊥平面BB1C
∵B1M?平面BB1C1C
∴AB⊥B1M.
(3)∵AB⊥平面BB1C1C
∴V=
×(
× 1×1×sin60°)×1=

则OM为△A1BN的中位线
∴OM∥A1N
∵A1N?平面AB1M,OM?平面AB1M
∴A1N∥平面AB1M.
(2)∵平面BB1C1C⊥平面ABC,而∠ABC=90°
∴AB⊥BC,AB?平面ABC
∴AB⊥平面BB1C
∵B1M?平面BB1C1C
∴AB⊥B1M.
(3)∵AB⊥平面BB1C1C
∴V=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 12 |
点评:证明线面平行关键是在平面内找到一条与已知直线平行的直线;证明线线垂直的关键是先把其中一条直线作为垂线另一条直线在一个平面内通过证明线面垂直得到;求三棱锥的体积较难时应该考虑是否换一个定点使其高与底面积都易求.

练习册系列答案
相关题目
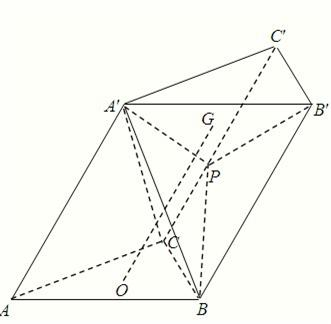 在斜三棱柱ABC-A′B′C′中,底面△ABC为正三角形,设AA′:AC=λ.顶点A′在底面ABC上的射影O是△ABC的中心,P为侧棱CC′中点,G为△PA′B′的重心.
在斜三棱柱ABC-A′B′C′中,底面△ABC为正三角形,设AA′:AC=λ.顶点A′在底面ABC上的射影O是△ABC的中心,P为侧棱CC′中点,G为△PA′B′的重心. (2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC=
(2008•武汉模拟)如图,在斜三棱柱ABC-A'B'C'中,∠ABC=90°,则侧面A'ACC'⊥侧面ABC,又AA'和底面所成60°的角,且AA'=2a,AB=BC= 时,求证:平面A′B′P⊥平面BB′C′C;
时,求证:平面A′B′P⊥平面BB′C′C;
 时,求证:平面A′B′P⊥平面BB′C′C;
时,求证:平面A′B′P⊥平面BB′C′C;
 .
.