题目内容
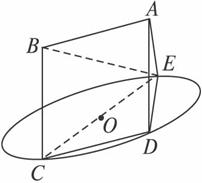
如图,边长为6的正方形ABCD所在平面,与面CDO交线为CD,线段CD为⊙O的弦,A在面CDO的射影是圆上并异于C、D的点E,CE为⊙O的直径,且AE=3.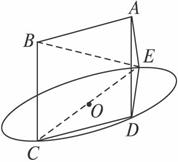
(1)求证:面ABCD⊥面ADE;
(2)求面ABCD与面CDE所成角的平面角的大小;
(3)求凸多边体ABCDE的体积.
答案:(1)证明: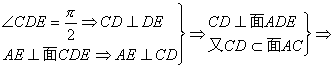 面AC⊥面ADE.
面AC⊥面ADE.
(2)解:由于DE⊥CD,再由三垂线定理得AD⊥CD,所以∠ADE为二面角的平面角,
由已知AE=3,AD=6,且在直角三角形中,得∠ADE=30°,
所以二面角的平面角为30°.
(3)解:凸多面体ABCDE为E—ABCD四棱锥,由(1)知面AC⊥面ADE,
所以在面ADE中过E作AD的垂线,垂足为F则EF⊥面AC,即为棱锥的高,可知EF=3![]() ,
,
所以VE—ABCD=![]() SABCD·EF=
SABCD·EF=![]() ×36×
×36×![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
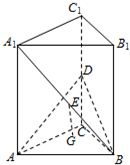 如图,边长为2的正方形A1ACC1绕直线CC1旋转90°得到正方形B1BCC1,D为CC1的中点,E为A1B的中点,G为△ADB的重心.
如图,边长为2的正方形A1ACC1绕直线CC1旋转90°得到正方形B1BCC1,D为CC1的中点,E为A1B的中点,G为△ADB的重心. 如图,边长为2的正方形ABCD所在平面为α,PA⊥平面α,PA=2,M、N分别是AD、BC的中点,MQ⊥PD于Q.
如图,边长为2的正方形ABCD所在平面为α,PA⊥平面α,PA=2,M、N分别是AD、BC的中点,MQ⊥PD于Q. 如图,边长为2的正方形内有一内切圆.在图形上随机撒一粒黄豆,则黄豆落到圆内的概率是( )
如图,边长为2的正方形内有一内切圆.在图形上随机撒一粒黄豆,则黄豆落到圆内的概率是( )