Question

解不等式|x-1|+|x-2|＞5.

Answer 1

分析：含两个或两个以上的绝对值不等式可根据x的不同取值情况,分别去掉绝对值的符号求解.

解析一：由|x-1|=0,|x-2|=0的根x=1及x=2把实数轴分成三个区间,在这三个区间上,根据绝对值的定义,代数式|x-1|+|x-2|有不同解析表达式,因而原不等式的解集是以下三个不等式组解集的并集.

(1)

分别解得不等式组(1)的解集为(-∞,-1);

不等式组(2)的解集为;

不等式组(3)的解集为(4,+∞).

所以原不等式组的解集为(-∞,-1)∪∪(4,+∞)=(-∞,-1)∪(4,+∞).

解法二：|x-1|+|x-2|＞5|x-1|+|x-2|-5＞0,设f(x)=|x-1|+|x-2|-5,

则f(x)=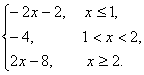

作出f(x)的图象为

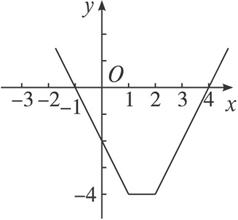
图1-2-1

f(x)为分段函数,其零点为-1,4,于是f(x)＞0?x＜-1或x＞4.

所以原不等式的解集为(-∞,-1)∪(4,+∞).