题目内容
用数学归纳法证明对n∈N＋都有
.
.见解析
①当n＝1时，左边＝
＝
，右边＝
＝，左边＝右边．
∴n＝1时，等式成立．
②假设＋
＋…＋
，
则n＝k＋1时，＋＋…＋
＋
＝
＋
＝
.
∴n＝k＋1时，等式成立．
由①②知
.
＝，右边＝＝，左边＝右边．∴n＝1时，等式成立．
②假设
＋＋…＋，则n＝k＋1时，
＋＋…＋＋＝＋＝
.∴n＝k＋1时，等式成立．
由①②知
.
练习册系列答案
相关题目
题目内容
.＝，右边＝＝，左边＝右边．＋＋…＋，＋＋…＋＋＝＋..
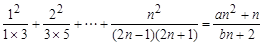对于一切n∈N*都成立？若存在，求出a,b的值，若不存在，请说明理由。
x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较
+
+
+…+
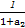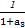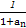与1的大小,并说明理由.
， (
)”时，在验证
成立时，左边应该是 ．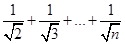
n∈N?)，g(n)＝2(
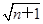－1)(n∈N?)．
时，在验证当
时，等式左边为（ ）
