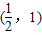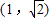题目内容
若点A的坐标为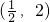 ,F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为
,F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为
- A.(0,0)
- B.

- C.
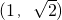
- D.(2,2)
B
分析:由抛物线的定义可先求F( ,0),根据MF+MA≥AF,可得A、M、F三点共线时,MF+MA取最小值AF,从而可求M
,0),根据MF+MA≥AF,可得A、M、F三点共线时,MF+MA取最小值AF,从而可求M
解答:由抛物线的定义可知F( ,0)
,0)
由于MF+MA≥AF
当AMF三点共线时,MF+MA取最小值AF
此时M(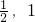 )
)
故选B.

点评:本题主要结合抛物线的定义,利用不等式MF+MA≥AF进行求解线段的最小(大)值问题,属于基本应用.
分析:由抛物线的定义可先求F(
 ,0),根据MF+MA≥AF,可得A、M、F三点共线时,MF+MA取最小值AF,从而可求M
,0),根据MF+MA≥AF,可得A、M、F三点共线时,MF+MA取最小值AF,从而可求M解答:由抛物线的定义可知F(
 ,0)
,0)由于MF+MA≥AF
当AMF三点共线时,MF+MA取最小值AF
此时M(
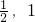 )
)故选B.

点评:本题主要结合抛物线的定义,利用不等式MF+MA≥AF进行求解线段的最小(大)值问题,属于基本应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
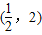 ,F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为( )
,F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为( )