题目内容
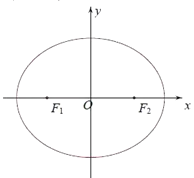
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 点的坐标;若不存在,请说明理由;
点的坐标;若不存在,请说明理由;
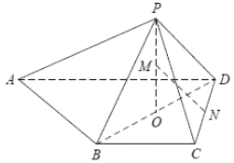
(3)设![]() 为椭圆
为椭圆![]() 上非长轴顶点的任意一点,
上非长轴顶点的任意一点,![]() 为线段
为线段![]() 上一点,若
上一点,若![]() 与
与![]() 的内切圆面积相等,求证:线段
的内切圆面积相等,求证:线段![]() 的长度为定值.
的长度为定值.
【答案】(1)![]() (2)存在,
(2)存在,![]() ,理由见解析;(3)证明见解析.
,理由见解析;(3)证明见解析.
【解析】
(1)设椭圆![]() 的焦距为
的焦距为![]() ,根据
,根据![]() 的面积计算出
的面积计算出![]() ,可设椭圆
,可设椭圆![]() 的标准方程为
的标准方程为![]() ,再将点
,再将点![]() 的坐标代入椭圆
的坐标代入椭圆![]() 的标准方程,求出
的标准方程,求出![]() 的值由此可求出椭圆
的值由此可求出椭圆![]() 的方程;
的方程;
(2)设点![]() ,
,![]() ,
,![]() ,由
,由![]() ,可得出
,可得出![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,代入
的方程联立,列出韦达定理,代入![]() ,求出实数
,求出实数![]() 的值,即可求出定点
的值,即可求出定点![]() 的坐标;
的坐标;
(3)设点![]() ,
,![]() ,
,![]() ,由题意得出
,由题意得出![]() ,化简得出
,化简得出![]() ,可求出正数
,可求出正数![]() 的值,从而得出结论.
的值,从而得出结论.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,因为
,因为![]() 的面积为
的面积为![]() ,所以
,所以![]() ,设椭圆
,设椭圆![]() 的方程为
的方程为![]() ,
,
将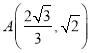 代入方程得
代入方程得![]() ,
,![]() ,
,
易知![]() ,所以
,所以![]() ,因此,椭圆
,因此,椭圆![]() 的方程为
的方程为![]() ;
;
(2)存在这样的点![]() 为
为![]() ,下面证明:
,下面证明:
设![]() ,
,![]() ,
,![]() ,所以要使得
,所以要使得![]() ,
,
即![]()
![]() ①;
①;
联立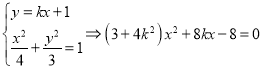 ,
,
由韦达定理得![]() ,
,![]() ,
,
代入可将①化简为![]() ,要使得式子关于
,要使得式子关于![]() 恒成立,即此时
恒成立,即此时![]() ,
,
所以点![]() ;
;
(3)设点![]() ,
,![]() ,
,![]() ,
,
因为内切圆面积相等,即圆半径相等,而内切圆半径公式为三角形面积的![]() 倍除以周长,所以
倍除以周长,所以![]() ,化简得
,化简得![]() ,
,
故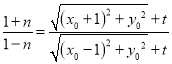 ,
,
因为![]() ,代入得
,代入得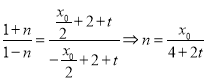 .
.
而![]() ,
,![]() ,
,
而![]() ,所以
,所以![]() ,即线段
,即线段![]() 的长度为定值
的长度为定值![]() .
.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】画糖是一种以糖为材料在石板上进行造型的民间艺术,常见于公园与旅游景点.某师傅制作了一种新造型糖画,为了合理定价,先进行试销售,其单价x(元)与销量y(个)相关数据如表:
单价x(元) | 8.5 | 9 | 9.5 | 10 | 10.5 |
销量y(个) | 12 | 11 | 9 | 7 | 6 |
(1)已知销量y与单价x具有线性相关关系,求y关于x的线性回归方程;
(2)若该新造型糖画每个的成本为5.7元,要使得进入售卖时利润最大,请利用所求出的线性回归方程确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程y![]() x中斜率和截距最小二乘法估计计算公式:
x中斜率和截距最小二乘法估计计算公式: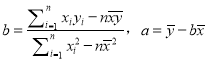 .参考数据:
.参考数据:![]() .
.