题目内容
已知函数f(x)= ,
,
(1)若a=4,求曲线f(x)在点(e,f(e))处的切线方程;
(2)求f(x)的极值;
(3)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围。
 ,
,(1)若a=4,求曲线f(x)在点(e,f(e))处的切线方程;
(2)求f(x)的极值;
(3)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围。
解:(1)∵a=4,
∴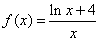 且
且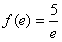 ,
,
又∵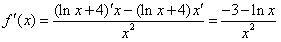 ,
,
∴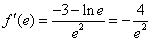 ,
,
∴f(x)在点(e,f(e))处的切线方程为: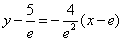 ,即4x+e2y-9e=0.
,即4x+e2y-9e=0.
(2)f(x)的定义域为(0,+∞),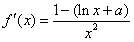 ,
,
令f′(x)=0得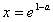 ,
,
当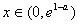 时,f′(x)>0,f(x)是增函数;
时,f′(x)>0,f(x)是增函数;
当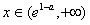 时,f′(x)<0,f(x)是减函数;
时,f′(x)<0,f(x)是减函数;
∴f(x)在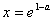 处取得极大值,即
处取得极大值,即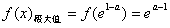 。
。
(3)①当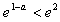 ,即a>-1时,由(2)知f(x)在(0,
,即a>-1时,由(2)知f(x)在(0,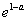 )上是增函数,在
)上是增函数,在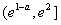 上是减函数,
上是减函数,
∴当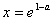 时,f(x)取得最大值,即
时,f(x)取得最大值,即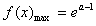 ;
;
又当x=e-a时,f(x)=0,当x∈(0,e-a]时,f(x)<0,
当x∈(e-a,e2]时,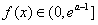 ,
,
所以f(x)的图象与g(x)=1的图象在(0,e2]上有公共点,
等价于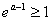 ,解得a≥1,
,解得a≥1,
又因为a>-1,所以a≥1;
②当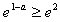 ,即a≤-1时,f(x)在(0,e2]上是增函数,
,即a≤-1时,f(x)在(0,e2]上是增函数,
∴f(x)在(0,e2]上的最大值为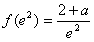 ,
,
∴原问题等价于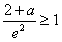 ,解得a≥e2-2,
,解得a≥e2-2,
又∵a≤-1,
∴无解;
综上,a的取值范围是a≥1。
∴
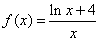 且
且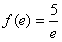 ,
,又∵
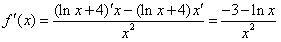 ,
, ∴
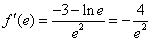 ,
,∴f(x)在点(e,f(e))处的切线方程为:
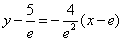 ,即4x+e2y-9e=0.
,即4x+e2y-9e=0.(2)f(x)的定义域为(0,+∞),
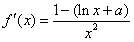 ,
,令f′(x)=0得
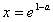 ,
,当
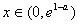 时,f′(x)>0,f(x)是增函数;
时,f′(x)>0,f(x)是增函数;当
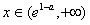 时,f′(x)<0,f(x)是减函数;
时,f′(x)<0,f(x)是减函数;∴f(x)在
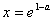 处取得极大值,即
处取得极大值,即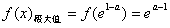 。
。(3)①当
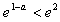 ,即a>-1时,由(2)知f(x)在(0,
,即a>-1时,由(2)知f(x)在(0,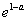 )上是增函数,在
)上是增函数,在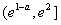 上是减函数,
上是减函数,∴当
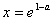 时,f(x)取得最大值,即
时,f(x)取得最大值,即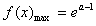 ;
;又当x=e-a时,f(x)=0,当x∈(0,e-a]时,f(x)<0,
当x∈(e-a,e2]时,
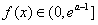 ,
,所以f(x)的图象与g(x)=1的图象在(0,e2]上有公共点,
等价于
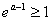 ,解得a≥1,
,解得a≥1,又因为a>-1,所以a≥1;
②当
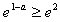 ,即a≤-1时,f(x)在(0,e2]上是增函数,
,即a≤-1时,f(x)在(0,e2]上是增函数,∴f(x)在(0,e2]上的最大值为
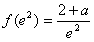 ,
,∴原问题等价于
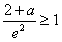 ,解得a≥e2-2,
,解得a≥e2-2,又∵a≤-1,
∴无解;
综上,a的取值范围是a≥1。

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|