��Ŀ����
7���躯��f��x�����䶨����D�ϵĵ�����Ϊf�䣨x�����������ʵ��a�ͺ���h��x��������h��x���������x��D������h��x����0��ʹ��f�䣨x��=h��x����x2-ax+1������ƺ���f��x���������ʦأ�a�������������ĸ���������f��x��=$\frac{1}{3}$x3-x2+x+1�� ��f��x��=lnx+$\frac{4}{x+1}$��
��f��x��=��x2-4x+5��ex�� ��f��x��=$\frac{{x}^{2}+x}{2x+1}$
���о������ʦأ�2���ĺ���Ϊ��������
| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �ڢۢ� | D�� | �٢ۢ� |
���� ��Ϊa=2���������������f��x���ĵ�����f�䣨x����Ȼ������ճ�f�䣨x��=h��x����x2-2x+1��������ʽ���ֱ����h��x����Ȼ��ȷ��h��x���Ƿ�����������x��D����h��x����0��
��� �⣺��f'��x��=x2-2x+1����f�䣨x��=h��x����x2-2x+1������x2-2x+1=h��x����x2-2x+1����
����h��x��=1��0���������������Ԣپ������ʦأ�2����
�ں���f��x��=lnx++$\frac{4}{x+1}$�Ķ�����Ϊ��0��+�ޣ���f�䣨x��=$\frac{1}{x}$-$\frac{4}{{��x+1��}^{2}}$=$\frac{{��x+1��}^{2}-4x}{x{•��x+1��}^{2}}$=$\frac{1}{x{•��x+1��}^{2}}$•��x2-2x+1����
����h��x��=$\frac{1}{x{•��x+1��}^{2}}$����x�ʣ�0��+�ޣ�ʱ��h��x����0�����Ԣھ������ʦأ�2����
��f'��x��=��2x-4��ex+��x2-4x+5��ex=��x2-2x+1��ex������h��x��=ex����Ϊh��x����0�����Ԣ۾������ʦأ�2����
��f�䣨x��=$\frac{��2x+1����2x+1��-2{��x}^{2}+1��}{{��2x+1��}^{2}}$=$\frac{{2x}^{2}+2x+1}{{��2x+1��}^{2}}$����f�䣨x��=$\frac{{2x}^{2}+2x+1}{{��2x+1��}^{2}•{��x}^{2}-2x+1��}$•��x2-2x+1����
��h��x��=$\frac{{2x}^{2}+2x+1}{{��2x+1��}^{2}•{��x}^{2}-2x+1��}$����Ϊh��1�������ڣ����Բ�����������x��D����h��x����0�����Ԣܲ��������ʦأ�2����
��ѡ��A��
���� ����Ŀ����ǵ����������Լ�ͨ��������h��x��������Ĺؼ���ͨ����ϵʽȷ������h��x���ı���ʽ��Ȼ���ж������Ƿ�����������е��⣮

| A�� | 30�� | B�� | 35�� | C�� | 20�� | D�� | 15�� |

| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |

| A�� | 0 | B�� | 1 | C�� | 3 | D�� | 4 |

| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
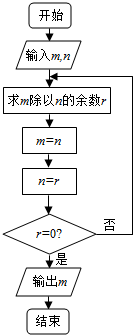
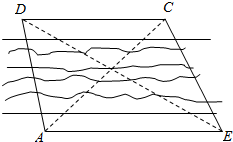 Ϊ�˲����Ӷ�����������C��D֮��ľ��룬�ںӰ���ȡ��A��B����BAC=45�㣬��DAC=75�㣬��ABD=30�㣬��DBC=45�㣬AB=$\sqrt{3}$ǧ�ף�A��B��C��D��ͬһ��ƽ���ڣ�����C��D֮��ľ��룮
Ϊ�˲����Ӷ�����������C��D֮��ľ��룬�ںӰ���ȡ��A��B����BAC=45�㣬��DAC=75�㣬��ABD=30�㣬��DBC=45�㣬AB=$\sqrt{3}$ǧ�ף�A��B��C��D��ͬһ��ƽ���ڣ�����C��D֮��ľ��룮