题目内容
在极坐标系中,圆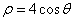 上的点到直线
上的点到直线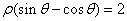 的最大距离为 .
的最大距离为 .
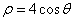 上的点到直线
上的点到直线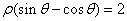 的最大距离为 .
的最大距离为 . 
试题分析:圆
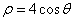 ,即ρ2=4ρcosθ,即 x2+y2=4x,
,即ρ2=4ρcosθ,即 x2+y2=4x,(x-2)2+y2=4,表示以C(2,0)为圆心,以2为半径的圆.
直线
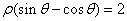 ,即ρsinθ-ρcosθ=2,即x-y+2=0,
,即ρsinθ-ρcosθ=2,即x-y+2=0,,圆心C(2,0)到直线x-y+2=0的距离等于
 ,
,故圆上的点到直线x-y+2=0的距离的最大值为
 。
。点评:中档题,将曲线的极坐标方程化为直角坐标方程,实现了“化生为熟”。利用数形结合思想,将最大距离确定为圆心到直线的距离加半径。

练习册系列答案
相关题目
 与曲线
与曲线 (
( 为参数)无公共点,则过点
为参数)无公共点,则过点 的直线与曲线
的直线与曲线 的公共点的个数为 .
的公共点的个数为 .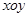 中,以原点O为极点,
中,以原点O为极点,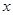 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线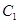 的极坐标方程为
的极坐标方程为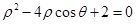 ,曲线
,曲线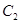 的参数方程为
的参数方程为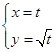 (
(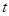 为参数,)
为参数,)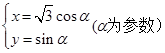 .
.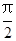 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系; ,
,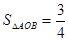 ;
; 的极坐标为
的极坐标为 ,下列所给出的四个坐标中不能表示点
,下列所给出的四个坐标中不能表示点



 与直线
与直线 相切,求实数a的值。
相切,求实数a的值。 上有n个点到曲线
上有n个点到曲线 的距离等于
的距离等于 ,则n=( )
,则n=( ) ,则
,则 的最大值是 。
的最大值是 。 经过点
经过点 ,圆心为直线
,圆心为直线 与极轴的交点,求圆
与极轴的交点,求圆