题目内容
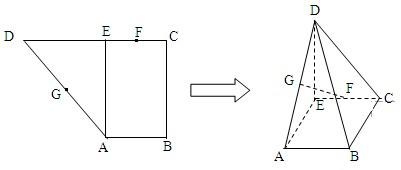
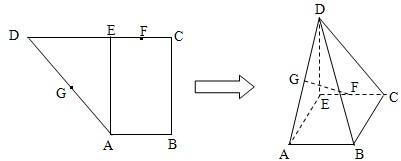
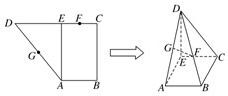
已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，CD=1+
，过A作AE⊥CD，垂足为E，G、F分别为AD、CE的中点，现将△ADE沿AE折叠，使得DE⊥EC．
（1）求证：BC⊥面CDE；
（2）求证：FG∥面BCD．
| 3 |
（1）求证：BC⊥面CDE；
（2）求证：FG∥面BCD．
证明：（1）由已知得：DE⊥AE，DE⊥EC，
∴DE⊥面ABCE∴DE⊥BC，又BC⊥CE，∴BC⊥面DCE；
（2）取AB中点H，连接GH，FH，
∴GH∥BD，FH∥BC，
∴GH∥面BCD，FH∥面BCD
∴面FHG∥面BCD，
∴GF∥面BCD
∴DE⊥面ABCE∴DE⊥BC，又BC⊥CE，∴BC⊥面DCE；
（2）取AB中点H，连接GH，FH，
∴GH∥BD，FH∥BC，
∴GH∥面BCD，FH∥面BCD
∴面FHG∥面BCD，
∴GF∥面BCD
练习册系列答案
相关题目
已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，CD=1+
已知直角梯形ABCD中，AB∥CD，∠BAD=90°，且AB=2，AD=3，CD=1，点E、F分别在AD、BC上，满足
如图，已知直角梯形ABCD的上底BC=