题目内容
5.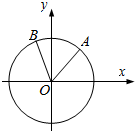 如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求
如图,在平面直角坐标系xOy中,以Ox轴为始边作角α和β,$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,其终边分别交单位圆于A,B两点.若A,B两点的横坐标分别是$\frac{3}{5}$,-$\frac{{\sqrt{2}}}{10}$. 试求(1)tanα,tanβ的值;
(2)∠AOB的值.
分析 (1)根据三角函数的定义即可求tanα,tanβ的值;
(2)∠AOB=β-α,利用两角和差的正切公式进行求解即可.
解答 解:(1)由条件知cosα=$\frac{3}{5}$,cosβ=-$\frac{{\sqrt{2}}}{10}$.
∵$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,
∴sinα=$\frac{4}{5}$,sinβ=$\sqrt{1-(-\frac{\sqrt{2}}{10})^{2}}$=$\frac{7\sqrt{2}}{10}$,
则tanα=$\frac{\frac{4}{5}}{\frac{3}{5}}$=$\frac{4}{3}$,tanβ=$\frac{\frac{7\sqrt{2}}{10}}{-\frac{\sqrt{2}}{10}}$=-7;
(2)∵∠AOB=β-α,
∴tan∠AOB=tan(β-α)=$\frac{tanβ-tanα}{1+tanβtanα}$=$\frac{-7-\frac{4}{3}}{1+(-7)×\frac{4}{3}}$=$\frac{-25}{-25}=1$,
∵$α∈({0,\frac{π}{2}}),β∈({\frac{π}{2},π})$,
∴0<β-α<π,
则β-α=$\frac{π}{4}$.
点评 本题主要考查三角函数的定义以及两角和差的正切公式的应用,考查学生的运算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{7}$ |
13.观察分析下表中的数据:
猜想一般凸多面体中,面数、顶点数、棱数:F、V、E所满足的等式是F+V=E+2.
| 多面体 | 面数(F) | 顶点数(V) | 棱数(E) |
| 三棱锥 | 5 | 6 | 9 |
| 五棱锥 | 6 | 6 | 10 |
| 立方体] | 6 | 8 | 12 |
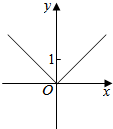
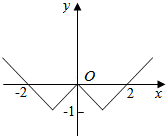
 函数f(x)的定义域为(a,b),其导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在区间(a,b)内极小值点的个数是( )
函数f(x)的定义域为(a,b),其导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在区间(a,b)内极小值点的个数是( )