题目内容
已知以下函数：（1）f（x）=3lnx；（2）f（x）=3ecosx；（3）f（x）=3ex；（4）f（x）=3cosx．
其中对于f（x）定义域内的任意一个自变量x1，都存在唯一一个自变量x2使
=3成立的函数是（ ）
其中对于f（x）定义域内的任意一个自变量x1，都存在唯一一个自变量x2使
| f(x1)f(x2) |
| A．（1）（2）（4） | B．（2）（3） | C．（3） | D．（4） |
对于（1）
=3即lnx1?lnx2=1，而当x1=1时就不存在x2使之成立，故不符合
（2）
=3即cosx1+cosx2=0，当x1任取一值时，存在无数个x2使之成立，故不符合
（3）符合题意
（4）
=3即cosx1?cosx2=1当x1任取一值时，存在无数个x2使之成立，故不符合
故选C
| 3lnx1?3lnx2 |
（2）
| 3ecosx1? 3ecosx2 |
（3）符合题意
（4）
| 3cosx1?3cosx2 |
故选C
练习册系列答案
科学实验活动册系列答案
相关题目
已知以下函数：（1）f（x）=3lnx；（2）f（x）=3ecosx；（3）f（x）=3ex；（4）f（x）=3cosx．
其中对于f（x）定义域内的任意一个自变量x1，都存在唯一一个自变量x2使
=3成立的函数是（ ）
其中对于f（x）定义域内的任意一个自变量x1，都存在唯一一个自变量x2使
| f(x1)f(x2) |
| A、（1）（2）（4） |
| B、（2）（3） |
| C、（3） |
| D、（4） |
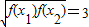成立的函数是（ ）
成立的函数是（ ）
成立的函数是（ ）
成立的函数是（ ）