题目内容
已知函数f(x)=asinx-x+b(a>0,b>0).
(1)求证:函数f(x)在区间[0,a+b]内至少有一个零点;
(2)若函数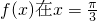 处取得极值.
处取得极值.
(i)不等式f(x)>sinx+cosx对任意 恒成立,求b的取值范围;
恒成立,求b的取值范围;
(ii)设△ABC的三个顶点A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,且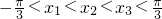 ,求证:f(sin2A+sin2C)<f(sin2B).
,求证:f(sin2A+sin2C)<f(sin2B).
(1)证明:∵函数f(x)=asinx-x+b,a、b均为正的常数
∴f(0)=b>0,f(a+b)=asin(a+b)-a-b+b=a[sin(a+b)-1]≤0
∴函数f(x)在(0,a+b]内至少有一个零点;
(2)解:f′(x)=acosx-1,
∵函数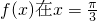 处取得极值,∴f′(
处取得极值,∴f′( )=0
)=0
∴acos -1=0,∴a=2
-1=0,∴a=2
(i)不等式f(x)>sinx+cosx等价于b>cosx-sinx+x对于任意 恒成立
恒成立
设g(x)=cosx-sinx+x,∴g′(x)=-sinx-cosx+1=- sin(x+
sin(x+ )+1
)+1
∵ ,∴
,∴ ,∴sin(x+
,∴sin(x+ )∈
)∈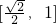
∴ sin(x+
sin(x+ )∈[1,
)∈[1, ]
]
∴g′(x)≤0
∴g(x)=cosx-sinx+x在[0, ]上是单调减函数,且最大值为g(0)=1
]上是单调减函数,且最大值为g(0)=1
∴b>1;
(ii)证明:当x∈(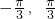 )时,cosx>
)时,cosx> ,∴f′(x)=2cosx-1>0,
,∴f′(x)=2cosx-1>0,
∴函数f(x)在(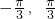 )上是单调递增函数
)上是单调递增函数
∵A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,且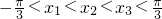 ,
,
∴y1<y2<y3
∵cos∠ABC=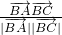 =
=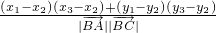
∴cos∠ABC<0
由余弦定理,cos∠ABC=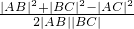 <0
<0
∴|AB|2+|BC|2<|AC|2
由正弦定理可得:sin2A+sin2C<sin2B
∴sin2A+sin2C、sin2B∈(0,1)⊆(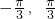 )
)
∵函数f(x)在(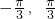 )上是单调递增函数
)上是单调递增函数
∴f(sin2A+sin2C)<f(sin2B).
分析:(1)利用f(0)=b>0,f(a+b)=asin(a+b)-a-b+b=a[sin(a+b)-1]≤0,可得函数f(x)在(0,a+b]内至少有一个零点;
(2)根据函数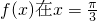 处取得极值,可得a=2
处取得极值,可得a=2
(i)不等式f(x)>sinx+cosx等价于b>cosx-sinx+x对于任意 恒成立,构造函数g(x)=cosx-sinx+x,求函数的最大值,即可求b的取值范围;
恒成立,构造函数g(x)=cosx-sinx+x,求函数的最大值,即可求b的取值范围;
(ii)确定函数f(x)在(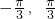 )上是单调递增函数,从而可得y1<y2<y3,利用向量的夹角公式、余弦定理、正弦定理可得sin2A+sin2C<sin2B,再利用函数f(x)在(
)上是单调递增函数,从而可得y1<y2<y3,利用向量的夹角公式、余弦定理、正弦定理可得sin2A+sin2C<sin2B,再利用函数f(x)在(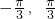 )上是单调递增函数,即可证得结论.
)上是单调递增函数,即可证得结论.
点评:本题考查函数的零点,考查导数知识的运用,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.
∴f(0)=b>0,f(a+b)=asin(a+b)-a-b+b=a[sin(a+b)-1]≤0
∴函数f(x)在(0,a+b]内至少有一个零点;
(2)解:f′(x)=acosx-1,
∵函数
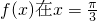 处取得极值,∴f′(
处取得极值,∴f′( )=0
)=0∴acos
 -1=0,∴a=2
-1=0,∴a=2(i)不等式f(x)>sinx+cosx等价于b>cosx-sinx+x对于任意
 恒成立
恒成立设g(x)=cosx-sinx+x,∴g′(x)=-sinx-cosx+1=-
 sin(x+
sin(x+ )+1
)+1∵
 ,∴
,∴ ,∴sin(x+
,∴sin(x+ )∈
)∈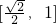
∴
 sin(x+
sin(x+ )∈[1,
)∈[1, ]
]∴g′(x)≤0
∴g(x)=cosx-sinx+x在[0,
 ]上是单调减函数,且最大值为g(0)=1
]上是单调减函数,且最大值为g(0)=1∴b>1;
(ii)证明:当x∈(
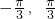 )时,cosx>
)时,cosx> ,∴f′(x)=2cosx-1>0,
,∴f′(x)=2cosx-1>0,∴函数f(x)在(
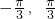 )上是单调递增函数
)上是单调递增函数∵A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,且
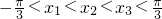 ,
,∴y1<y2<y3
∵cos∠ABC=
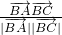 =
=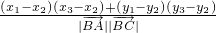
∴cos∠ABC<0
由余弦定理,cos∠ABC=
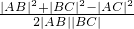 <0
<0∴|AB|2+|BC|2<|AC|2
由正弦定理可得:sin2A+sin2C<sin2B
∴sin2A+sin2C、sin2B∈(0,1)⊆(
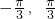 )
)∵函数f(x)在(
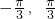 )上是单调递增函数
)上是单调递增函数∴f(sin2A+sin2C)<f(sin2B).
分析:(1)利用f(0)=b>0,f(a+b)=asin(a+b)-a-b+b=a[sin(a+b)-1]≤0,可得函数f(x)在(0,a+b]内至少有一个零点;
(2)根据函数
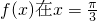 处取得极值,可得a=2
处取得极值,可得a=2(i)不等式f(x)>sinx+cosx等价于b>cosx-sinx+x对于任意
 恒成立,构造函数g(x)=cosx-sinx+x,求函数的最大值,即可求b的取值范围;
恒成立,构造函数g(x)=cosx-sinx+x,求函数的最大值,即可求b的取值范围;(ii)确定函数f(x)在(
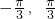 )上是单调递增函数,从而可得y1<y2<y3,利用向量的夹角公式、余弦定理、正弦定理可得sin2A+sin2C<sin2B,再利用函数f(x)在(
)上是单调递增函数,从而可得y1<y2<y3,利用向量的夹角公式、余弦定理、正弦定理可得sin2A+sin2C<sin2B,再利用函数f(x)在(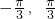 )上是单调递增函数,即可证得结论.
)上是单调递增函数,即可证得结论.点评:本题考查函数的零点,考查导数知识的运用,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目