Question

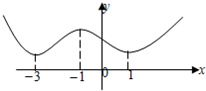
如图为函数f（x）的图象，f′（x）为函数f（x）的导函数，则不等式x•f′（x）＜0的解集为________．

Answer 1

（-∞，0）
分析：由函数的图象可以看出，f′（x）在R上恒为正，由此关系解不等式x•f′（x）＜0，即可得到其解集
解答：由图，导数恒为正
∵x•f′（x）＜0
∴x＜0
故不等式x•f′（x）＜0的解集为（-∞，0）
故答案为（-∞，0）
点评：本题利用导数研究函数的单调性，解题的关键是理解并掌握函数的导数的符号与函数的单调性的关系，本题利用图形告诉函数导数的符号，形式新颖，且利用图象所给的关系解不等式，设计巧妙，是近几年高考命题的方向，在这几年的高考试题命题中，有一个很显著的特征就是加强了对图象的考查，题后要注意总结本题的特点．