题目内容
给出下列命题:
①命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”;
②“x=-1”是“x2-5x-6=0”的必要不充分条件;
③命题“?x∈R,使得x2+x-1<0”的否定是:“?x∈R,均有x2+x-1>0”;
④命题“若x=y,则sinx=siny”的逆否命题为真命题.
其中所有正确命题的序号是
①命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”;
②“x=-1”是“x2-5x-6=0”的必要不充分条件;
③命题“?x∈R,使得x2+x-1<0”的否定是:“?x∈R,均有x2+x-1>0”;
④命题“若x=y,则sinx=siny”的逆否命题为真命题.
其中所有正确命题的序号是
④
④
.分析:①根据命题的否命题和原命题之间的关系判断.②利用充分条件和必要条件的定义判断.③利用特称命题的否定判断.④利用逆否命题的等价性进行判断.
解答:解:①根据否命题的定义可知命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1”,所以①错误.
②由x2-5x-6=0得x=-1或x=6,所以②“x=-1”是“x2-5x-6=0”的充分不必要条件,所以②错误.
③根据特称命题的否定是全称命题得命题“?x∈R,使得x2+x-1<0”的否定是:“?x∈R,均有x2+x-1≥0”,所以③错误.
④根据逆否命题和原命题为等价命题可知原命题正确,所以命题“若x=y,则sinx=siny”的逆否命题为真命题,所以④正确.
故答案为:④.
②由x2-5x-6=0得x=-1或x=6,所以②“x=-1”是“x2-5x-6=0”的充分不必要条件,所以②错误.
③根据特称命题的否定是全称命题得命题“?x∈R,使得x2+x-1<0”的否定是:“?x∈R,均有x2+x-1≥0”,所以③错误.
④根据逆否命题和原命题为等价命题可知原命题正确,所以命题“若x=y,则sinx=siny”的逆否命题为真命题,所以④正确.
故答案为:④.
点评:本题主要考查命题的真假判断,以及四种命题的真假关系的判断,比较基础.

练习册系列答案
相关题目
 y =
y = 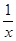 的一个交点;
的一个交点; 的一个交点
的一个交点 的一个交点
的一个交点 (
( 的一个交点;
的一个交点; 的一个交点;
的一个交点; 的一个交点;
的一个交点; (
(